1 3 Plus 1 3
couponhaat
Sep 17, 2025 · 6 min read
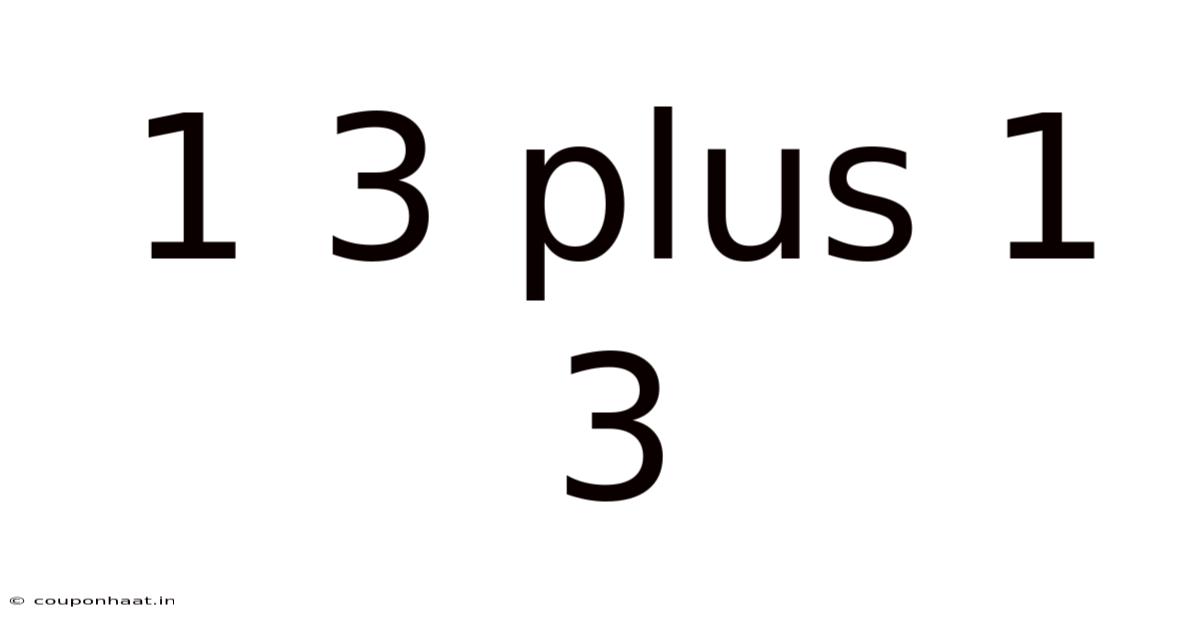
Table of Contents
Decoding 1/3 Plus 1/3: A Deep Dive into Fractions and Their Applications
Fractions are a fundamental concept in mathematics, forming the building blocks for more advanced topics like algebra, calculus, and beyond. Understanding how to add, subtract, multiply, and divide fractions is crucial for success in many academic and practical scenarios. This article will delve into the seemingly simple problem of "1/3 plus 1/3," exploring not just the solution but the underlying principles, common misconceptions, and real-world applications. We'll unpack the process step-by-step, catering to various learning styles and ensuring a comprehensive understanding for everyone.
Introduction: Understanding Fractions
Before tackling the specific problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For instance, in the fraction 1/3, the numerator is 1 and the denominator is 3, signifying one part out of three equal parts.
Adding Fractions: A Step-by-Step Guide
Adding fractions is straightforward when the denominators are the same. In our case, we have 1/3 + 1/3. Since the denominators are identical (both are 3), we can simply add the numerators and keep the denominator the same.
- Step 1: Check the denominators. Both denominators are 3. This is crucial for direct addition.
- Step 2: Add the numerators. 1 + 1 = 2.
- Step 3: Keep the denominator the same. The denominator remains 3.
- Step 4: Simplify the result. Our answer is 2/3. This fraction is already in its simplest form because 2 and 3 have no common factors other than 1.
Therefore, 1/3 + 1/3 = 2/3.
Visual Representation: Making it Concrete
Visual aids can significantly improve understanding, especially when dealing with abstract concepts like fractions. Imagine a pizza cut into three equal slices. 1/3 represents one slice. If you add another 1/3 (another slice), you now have 2/3 of the pizza. This simple visualization helps solidify the concept and makes the addition process more intuitive. Similarly, you could use bars, circles, or any other divisible shape to illustrate the concept.
What if the Denominators Were Different?
Adding fractions with different denominators requires an extra step: finding a common denominator. Let's say we want to add 1/3 and 1/2. We need to find a number that is a multiple of both 3 and 2. The least common multiple (LCM) of 3 and 2 is 6.
- Step 1: Find the least common denominator (LCD). The LCD of 3 and 2 is 6.
- Step 2: Convert the fractions to equivalent fractions with the LCD. To convert 1/3 to an equivalent fraction with a denominator of 6, we multiply both the numerator and denominator by 2 (1/3 * 2/2 = 2/6). To convert 1/2 to an equivalent fraction with a denominator of 6, we multiply both the numerator and denominator by 3 (1/2 * 3/3 = 3/6).
- Step 3: Add the numerators. 2 + 3 = 5.
- Step 4: Keep the denominator the same. The denominator remains 6.
- Step 5: Simplify the result (if possible). The answer is 5/6.
Therefore, 1/3 + 1/2 = 5/6.
Real-World Applications of Fraction Addition
Understanding fraction addition isn't just an academic exercise; it has numerous practical applications in everyday life. Here are a few examples:
- Cooking and Baking: Recipes often require fractional measurements. Adding ingredients involves adding fractions. For example, a recipe might call for 1/3 cup of sugar and 1/3 cup of flour, requiring you to add those fractions to determine the total amount of dry ingredients.
- Construction and Engineering: In construction, precise measurements are critical. Adding fractional lengths of materials (e.g., wood, metal) is essential for accurate calculations.
- Finance and Budgeting: Managing finances often involves dealing with fractions of money. For instance, calculating how much you've saved from your budget involves adding fractional amounts.
- Data Analysis: Many statistical analyses rely on understanding and manipulating fractions and proportions. Interpreting data often involves adding fractional components of a whole.
- Time Management: Dividing your time efficiently often involves working with fractions of an hour or a day. Adding up fractional units of time is necessary for scheduling and task management.
Common Misconceptions about Fractions
Several common misconceptions can hinder a thorough understanding of fractions:
- Adding denominators: A common mistake is adding both the numerators and the denominators. Remember, only the numerators are added when the denominators are the same.
- Improper simplification: Failing to simplify the final answer to its lowest terms can lead to inaccurate results. Always reduce the fraction to its simplest form by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
- Incorrect LCM calculation: When adding fractions with different denominators, accurately finding the least common multiple (LCM) is crucial. Incorrect LCM calculation will lead to incorrect results.
- Ignoring the concept of the whole: Sometimes, students struggle to connect the fraction to the concept of the whole. Remembering the "whole" helps understand the magnitude of the fraction.
Frequently Asked Questions (FAQ)
-
Q: Can I add fractions with different denominators without finding a common denominator? A: No, you cannot directly add fractions with different denominators. You must first convert them to equivalent fractions with a common denominator.
-
Q: What if the result of adding fractions is an improper fraction (numerator is larger than the denominator)? A: An improper fraction can be converted into a mixed number. For example, 5/3 is an improper fraction which can be written as 1 2/3 (one and two-thirds).
-
Q: How do I subtract fractions? A: Subtracting fractions follows a similar process to addition. If the denominators are the same, subtract the numerators and keep the denominator the same. If the denominators are different, find a common denominator first, then subtract the numerators.
-
Q: Are there online tools or calculators to help with fraction addition? A: Yes, many online resources and calculators can assist with fraction addition and other fraction operations. These tools can be helpful for checking answers and gaining additional practice.
Conclusion: Mastering Fractions for a Brighter Future
Mastering fractions is essential for success in mathematics and its countless real-world applications. The seemingly simple problem of "1/3 plus 1/3" serves as a gateway to understanding the broader principles of fraction arithmetic. By grasping the fundamental concepts and avoiding common pitfalls, you can build a solid foundation for more advanced mathematical concepts and confidently apply your knowledge to diverse situations. Remember the visual representations, practice consistently, and don't hesitate to seek help when needed. The journey to mastering fractions is rewarding, opening doors to a deeper appreciation of mathematics and its practical power. Embrace the challenge, and you'll be surprised at how much you can achieve.
Latest Posts
Latest Posts
-
Examples Of Tone In Poetry
Sep 17, 2025
-
Ruler In Mm Actual Size
Sep 17, 2025
-
The Love Of Good Woman
Sep 17, 2025
-
Bohr Rutherford Diagram For Potassium
Sep 17, 2025
-
61 Cm Converted To Inches
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Plus 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.