13 20 As A Percent
couponhaat
Sep 12, 2025 · 5 min read
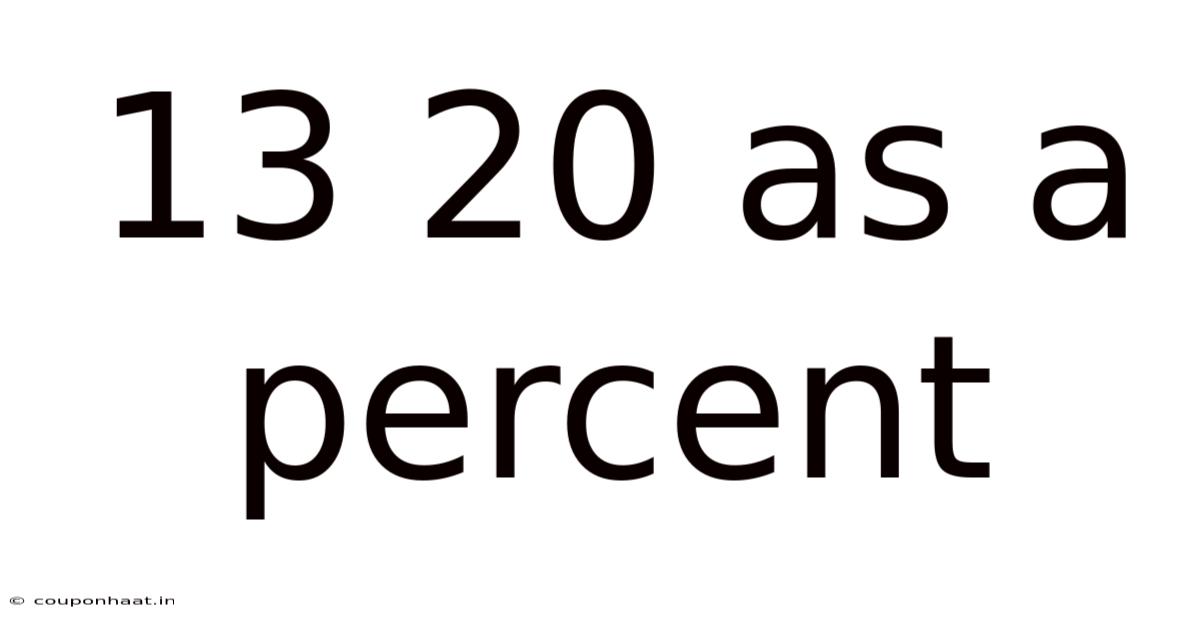
Table of Contents
Understanding 13/20 as a Percentage: A Comprehensive Guide
What does 13 out of 20 represent as a percentage? This seemingly simple question unlocks a fundamental concept in mathematics—converting fractions to percentages. This guide will not only show you how to calculate 13/20 as a percentage but also delve into the underlying principles, provide practical examples, and explore related concepts to solidify your understanding. This will equip you with the skills to confidently tackle similar percentage calculations in various contexts.
Introduction: Fractions, Decimals, and Percentages
Before diving into the specific calculation of 13/20 as a percentage, let's clarify the relationship between fractions, decimals, and percentages. These three represent different ways to express parts of a whole.
-
Fraction: A fraction shows a part of a whole using a numerator (top number) and a denominator (bottom number). For example, 13/20 means 13 parts out of a total of 20 parts.
-
Decimal: A decimal uses a base-10 system to represent parts of a whole. It uses a decimal point to separate the whole number from the fractional part.
-
Percentage: A percentage represents a fraction or decimal as parts per hundred. The symbol "%" indicates "per hundred."
Calculating 13/20 as a Percentage: Step-by-Step
There are two primary methods to convert the fraction 13/20 into a percentage:
Method 1: Using Division
-
Divide the numerator by the denominator: Divide 13 by 20. This gives you 0.65.
-
Multiply by 100: Multiply the decimal result (0.65) by 100 to convert it to a percentage. This gives you 65.
-
Add the percentage symbol: Add the "%" symbol to indicate that the result is a percentage.
Therefore, 13/20 is equal to 65%.
Method 2: Using Proportions
This method relies on setting up a proportion:
-
Set up a proportion: We want to find the percentage, which is a number out of 100. So we set up the proportion: 13/20 = x/100, where 'x' represents the percentage we want to find.
-
Cross-multiply: Multiply 13 by 100 and 20 by x: 1300 = 20x
-
Solve for x: Divide both sides by 20: x = 1300/20 = 65
Therefore, x = 65, meaning 13/20 is equal to 65%.
Understanding the Result: What does 65% mean?
65% signifies that 13 represents 65 parts out of every 100 parts of the whole. Imagine you have 100 apples, and 65 of them are red. The fraction of red apples would be 65/100, which is equivalent to 65%. Similarly, if you scored 13 out of 20 on a test, you achieved a score of 65%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-life scenarios:
-
Academic Performance: Calculating grades, test scores, and overall academic progress.
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
-
Shopping: Determining discounts, sales tax, and comparing prices.
-
Statistics: Representing data visually using pie charts, bar graphs, and other visual aids.
-
Science: Expressing experimental results, data analysis, and error margins.
Further Exploration: Related Percentage Calculations
Let's explore some related percentage calculations to broaden your understanding:
-
Calculating a Percentage of a Number: If you need to find 65% of a certain number (e.g., 65% of 50), you would multiply the number by the decimal equivalent of the percentage (0.65 * 50 = 32.5).
-
Finding the Percentage Increase or Decrease: Suppose a value increases from 20 to 26. The percentage increase is calculated as [(26-20)/20] * 100 = 30%. Similarly, a decrease from 20 to 15 would represent a 25% decrease.
-
Converting Percentages to Fractions and Decimals: To convert a percentage to a decimal, divide the percentage by 100 (e.g., 65% = 0.65). To convert a percentage to a fraction, write the percentage as the numerator and 100 as the denominator (e.g., 65% = 65/100 = 13/20).
Frequently Asked Questions (FAQs)
Q1: Why is it important to learn about percentages?
A1: Percentages are fundamental to understanding and interpreting numerical data in everyday life, across various fields including finance, education, science, and more. Mastering percentage calculations improves your analytical and problem-solving skills.
Q2: Are there any shortcuts for calculating percentages?
A2: Yes, for certain percentages like 10%, 25%, or 50%, mental math shortcuts can be used. For example, 10% of a number is simply one-tenth of that number. However, for more complex percentages, the methods described above are more reliable.
Q3: What if the fraction is not easily simplified?
A3: If you encounter a fraction that's not easily simplified, you can still use the division method to convert it into a percentage. Use a calculator if needed for more accuracy.
Q4: Can I use a calculator for these calculations?
A4: Absolutely! Calculators are valuable tools for percentage calculations, particularly when dealing with larger numbers or more complex fractions. They ensure accuracy and speed up the process.
Q5: How can I improve my understanding of percentages further?
A5: Practice regularly with different examples and problems. Work through various scenarios, including those involving percentage increases, decreases, and finding percentages of numbers. Use online resources, textbooks, or educational apps to enhance your learning.
Conclusion: Mastering the Fundamentals of Percentages
This comprehensive guide has shown you how to calculate 13/20 as a percentage, which is 65%. We've explored the underlying principles, demonstrated different calculation methods, and highlighted various applications of percentage calculations in everyday life. Remember, understanding percentages is a valuable skill that will serve you well in various academic and professional pursuits. By consistently practicing and applying these concepts, you can build a strong foundation in mathematics and confidently tackle similar percentage-related problems in the future. The ability to convert fractions to percentages, and vice versa, unlocks a deeper understanding of numerical representation and quantitative analysis. Remember to continue practicing to further solidify your understanding of this essential mathematical concept.
Latest Posts
Latest Posts
-
Instantaneous Rate Of Change Calculator
Sep 12, 2025
-
St Mary Ethiopian Orthodox Church
Sep 12, 2025
-
What Does P P M Stand For
Sep 12, 2025
-
Australia Flag Vs Nz Flag
Sep 12, 2025
-
What Is Battery Vs Assault
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 13 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.