16 20 As A Percent
couponhaat
Sep 13, 2025 · 5 min read
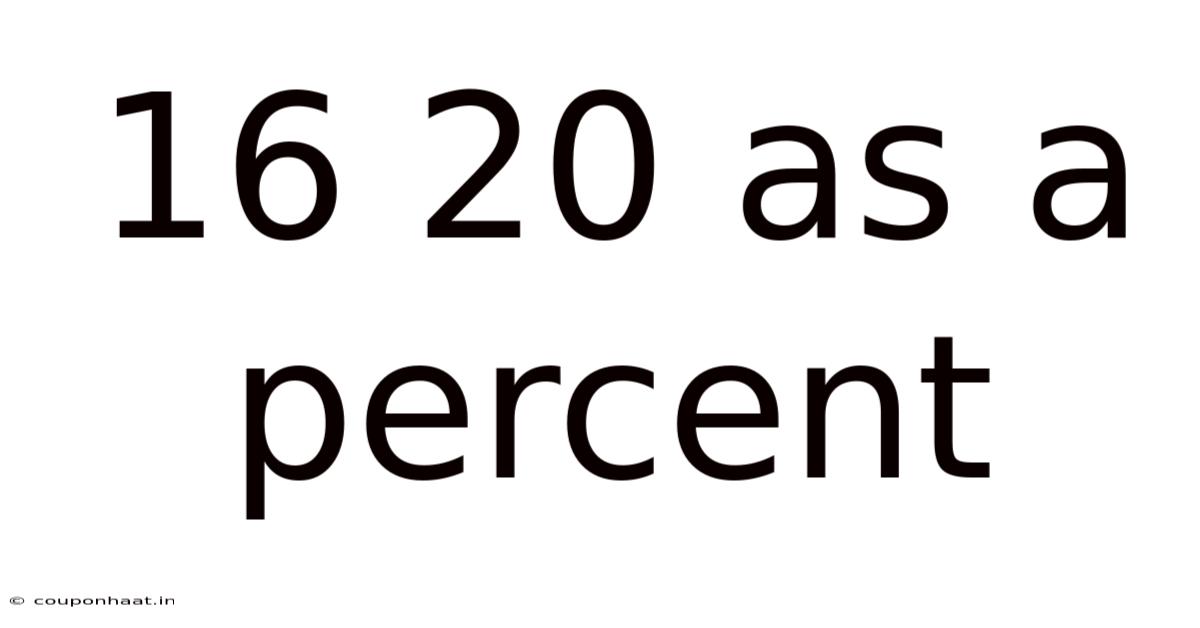
Table of Contents
16/20 as a Percent: A Comprehensive Guide to Understanding Percentages
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts in shopping to analyzing financial data. This article delves into the process of converting fractions to percentages, focusing specifically on expressing 16/20 as a percentage. We'll cover the calculation, explain the underlying principles, and explore various real-world applications, making the concept easily understandable for everyone, regardless of their mathematical background.
Understanding Fractions and Percentages
Before we dive into converting 16/20 into a percentage, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. The top number (numerator) indicates the portion being considered, while the bottom number (denominator) represents the total number of parts. For example, in the fraction 16/20, 16 represents the part and 20 represents the whole.
A percentage, denoted by the symbol %, represents a fraction where the denominator is always 100. Essentially, a percentage indicates the proportion of a quantity relative to 100. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating 16/20 as a Percentage: Step-by-Step Guide
The conversion of 16/20 to a percentage involves two simple steps:
Step 1: Convert the fraction to a decimal.
To do this, we divide the numerator (16) by the denominator (20):
16 ÷ 20 = 0.8
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.8 x 100 = 80%
Therefore, 16/20 is equal to 80%.
Simplifying Fractions Before Conversion
While the above method works perfectly, we can simplify the fraction before converting it to a decimal, making the calculation even easier. In this case, both 16 and 20 are divisible by 4:
16 ÷ 4 = 4 20 ÷ 4 = 5
This simplifies the fraction to 4/5. Now, we can proceed with the conversion:
4 ÷ 5 = 0.8
0.8 x 100 = 80%
This demonstrates that simplifying the fraction beforehand doesn't alter the final percentage; it merely simplifies the arithmetic involved.
Understanding the Concept: Real-world Applications
The concept of expressing a fraction as a percentage is incredibly useful in numerous real-world scenarios. Let's explore a few examples:
-
Academic Performance: Imagine a student scores 16 out of 20 marks on a test. Converting this to a percentage (80%) provides a clear and easily understandable representation of their performance. This allows for easy comparison with other students and helps track progress over time.
-
Sales and Discounts: A store offers a 20% discount on an item. If the original price is $100, the discount amount is calculated as 20% of $100, which is $20. Understanding percentages is crucial for calculating discounts and sale prices.
-
Financial Analysis: In finance, percentages are used extensively to represent various financial ratios, such as profit margins, return on investment (ROI), and interest rates. Understanding these percentages helps in making informed financial decisions.
-
Statistical Data: Percentages are vital in representing statistical data. For example, the percentage of a population that supports a particular political candidate or the percentage of students who pass a particular exam. These percentages provide a concise and easily interpretable summary of the data.
-
Data Representation in Charts and Graphs: Percentages are frequently used in charts and graphs to visually represent data proportions. Pie charts, for example, use percentages to show the proportion of each category within a whole.
Further Exploration: Beyond 16/20
Understanding the conversion of 16/20 to a percentage allows us to easily tackle similar problems. For instance, let's consider another example:
Converting 12/15 to a percentage:
-
Simplify the fraction: Both 12 and 15 are divisible by 3, resulting in 4/5.
-
Convert to decimal: 4 ÷ 5 = 0.8
-
Convert to percentage: 0.8 x 100 = 80%
Notice that both 16/20 and 12/15 result in the same percentage (80%). This highlights that equivalent fractions always result in the same percentage value.
Frequently Asked Questions (FAQ)
Q1: What if the denominator isn't a factor of 100?
A: If the denominator is not a factor of 100 (e.g., 16/23), you still follow the same steps: divide the numerator by the denominator to obtain the decimal and then multiply by 100 to convert it to a percentage. You might get a decimal percentage (e.g., 69.57%).
Q2: How do I convert a percentage back to a fraction?
A: To convert a percentage back to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 80% becomes 80/100, which simplifies to 4/5.
Q3: Are there any online tools to help with percentage calculations?
A: Yes, many online calculators and converters are readily available to assist with percentage calculations, including converting fractions to percentages.
Q4: What are some common errors to avoid when converting fractions to percentages?
A: Common errors include incorrectly dividing the numerator by the denominator or forgetting to multiply the decimal by 100 before adding the percentage symbol. Careful attention to these steps is crucial to avoid inaccuracies.
Conclusion
Converting fractions to percentages is a crucial skill that has far-reaching applications. The conversion of 16/20 to 80% demonstrates a straightforward process involving dividing the numerator by the denominator and then multiplying by 100. This skill isn't just limited to classroom settings; it’s a practical tool for everyday life, from calculating discounts to understanding financial reports. By mastering this concept, you equip yourself with a valuable tool for navigating numerous situations requiring numerical comprehension and analysis. Remember to practice consistently and you will become proficient in converting fractions to percentages effortlessly. Understanding this seemingly simple concept unlocks a deeper understanding of the world around us, filled with percentages expressing proportions and relationships in countless contexts.
Latest Posts
Latest Posts
-
French Words Beginning With L
Sep 13, 2025
-
Lewis Structure For Magnesium Chloride
Sep 13, 2025
-
British Gallon Vs Us Gallon
Sep 13, 2025
-
Difference Between Prejudice And Stereotype
Sep 13, 2025
-
Is A Cylinder A Prism
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 16 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.