2 1 4 X 2
couponhaat
Sep 14, 2025 · 6 min read
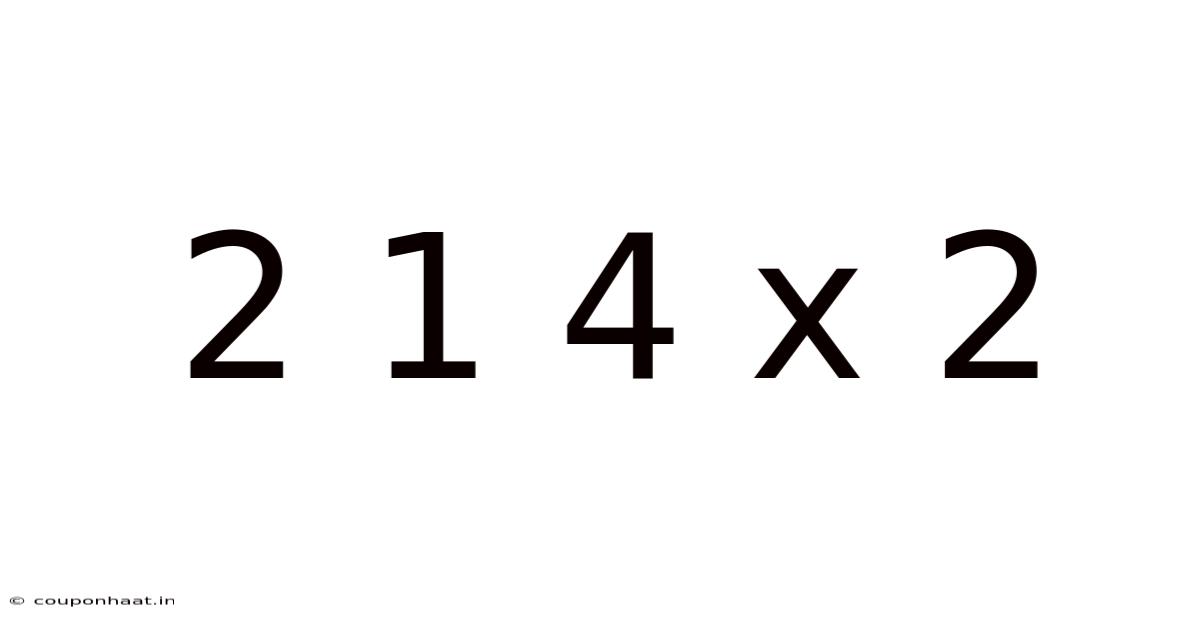
Table of Contents
Decoding 2 1 4 x 2: A Deep Dive into Mathematical Operations and Problem-Solving Strategies
This article explores the seemingly simple mathematical expression "2 1 4 x 2," delving beyond the immediate calculation to uncover the underlying principles, potential interpretations, and problem-solving strategies involved. We'll examine different approaches to solving this, address common misunderstandings, and explore the broader mathematical concepts at play. This will provide a comprehensive understanding, valuable not only for students grappling with basic arithmetic but also for those interested in exploring the intricacies of mathematical notation and ambiguity resolution.
Understanding the Ambiguity: Order of Operations
The core challenge presented by "2 1 4 x 2" lies in its ambiguity. Unlike a clearly structured expression like "(2 + 1 + 4) x 2," this expression lacks explicit parentheses or other indicators to define the order of operations. This is where the understanding of PEMDAS/BODMAS (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) becomes crucial. This mnemonic dictates the sequence in which mathematical operations should be performed.
Approach 1: Interpreting as a Concatenated Number
One possible interpretation is to treat "2 1 4" as a single concatenated number, resulting in the expression 214 x 2. This approach simplifies the problem significantly.
Calculation:
214 x 2 = 428
This interpretation, while straightforward, might not be the intended meaning, especially in the context of more complex mathematical problems where numbers and operators are intermingled.
Approach 2: Exploring Different Order of Operations
In the absence of parentheses, the ambiguity allows for exploring multiple interpretations based on applying different orders of operation. This highlights the importance of clear notation in mathematics. Let's examine various possibilities:
Scenario A: Multiplication First
If we prioritize multiplication according to PEMDAS/BODMAS, we could interpret the expression as:
2 + (1 + 4 x 2) = 2 + (1 + 8) = 2 + 9 = 11
This approach prioritizes the multiplication operation (4 x 2) before addition.
Scenario B: Addition First (Left to Right)
Alternatively, we could interpret the expression by performing addition from left to right before multiplication:
(2 + 1 + 4) x 2 = 7 x 2 = 14
This interpretation prioritizes addition operations before multiplication, performing the additions before multiplying the result by 2. This is potentially a less common approach, as it deviates from the standard order of operations.
Scenario C: Mixed Operations (Left to Right)
We could also explore different operation order combinations from left to right. For example:
(2 + 1) x 4 x 2 = 3 x 4 x 2 = 12 x 2 = 24
These various scenarios demonstrate how the lack of clear notation in the original expression can lead to different numerical results.
The Importance of Clear Notation
The ambiguity highlighted by the expression "2 1 4 x 2" underlines the critical role of precise mathematical notation. Clear use of parentheses, brackets, or other grouping symbols eliminates potential misinterpretations and ensures that everyone understands the intended order of operations. For instance, rewriting the expression with parentheses clarifies the intended order of operations:
- (2 + 1 + 4) x 2 = 14
- 2 + (1 + 4) x 2 = 11
- 2 + 1 + 4 x 2 = 11 (Multiplication before addition according to standard PEMDAS/BODMAS)
- (2 + 1) x (4 x 2) = 24
This highlights how seemingly minor details in notation can significantly alter the final result.
Extending the Concept: Application in Programming
The issue of order of operations isn't limited to basic arithmetic; it extends to programming and computer science. Programming languages have defined rules for operator precedence, mirroring PEMDAS/BODMAS, although the specific precedence of operators might vary slightly across different languages. Understanding operator precedence is vital to write correct and predictable code. Failure to account for operator precedence can lead to unexpected and potentially disastrous outcomes.
Exploring Related Mathematical Concepts
This simple expression opens doors to explore various interconnected mathematical concepts:
- Arithmetic Operations: This problem reinforces the understanding of basic arithmetic operations – addition and multiplication.
- Order of Operations: The ambiguity underscores the importance of the order of operations, guiding us through the correct sequence of calculations.
- Mathematical Notation: The problem highlights the critical role of clear and precise mathematical notation in avoiding ambiguity and ensuring accurate results.
- Algebraic Expressions: The problem can be easily extended to include algebraic variables, creating algebraic expressions where the numbers are replaced with variables. This allows for a deeper exploration of algebraic manipulation and simplification.
- Problem-Solving Strategies: The multiple interpretations and solution approaches encourage systematic and creative problem-solving strategies.
Frequently Asked Questions (FAQ)
Q1: What is the correct answer to 2 1 4 x 2?
A1: There's no single "correct" answer without clarifying the order of operations using parentheses or other unambiguous notation. The different interpretations we explored above all lead to valid results based on different assumptions about the intended calculation.
Q2: Why is clear notation so important in mathematics?
A2: Clear notation prevents ambiguity and ensures everyone interprets a mathematical expression in the same way. Without clear notation, different interpretations can lead to vastly different results. This is crucial in mathematics, science, engineering, and computing, where precise calculations are essential.
Q3: Can this expression be used to teach children about order of operations?
A3: Yes, this expression serves as an excellent example to teach children the importance of order of operations. It visually demonstrates how different interpretations, based on varying order of operation assumptions, result in distinct outcomes, highlighting the necessity of clear notation and using parenthesis or brackets for clarification. Using this example, teachers can emphasize the significance of correctly applying PEMDAS/BODMAS to achieve consistent and accurate results.
Q4: How does this relate to more advanced mathematical concepts?
A4: The underlying principles of order of operations and unambiguous notation extend to much more advanced mathematical concepts, including matrix operations, calculus, and abstract algebra. The emphasis on clarity and consistent interpretation remains paramount across all branches of mathematics.
Q5: Are there any real-world applications of understanding order of operations?
A5: Yes, understanding order of operations is essential in many real-world applications, including accounting, engineering, programming, physics, and chemistry. Misinterpreting the order of operations can lead to incorrect calculations, potentially causing significant errors and consequences. Therefore, a firm grasp of the order of operations is essential for accuracy and reliability in these diverse fields.
Conclusion
The seemingly simple expression "2 1 4 x 2" unexpectedly reveals the profound importance of clear mathematical notation and a thorough understanding of the order of operations. While the expression itself is ambiguous, the process of analyzing its various interpretations provides a valuable lesson on problem-solving strategies and the critical role of precision in mathematics. The exploration of this seemingly straightforward calculation extends far beyond simple arithmetic, illustrating the interconnectedness of mathematical concepts and emphasizing the importance of clear communication and unambiguous notation in all aspects of mathematics and its real-world applications. By carefully examining the different approaches and considering the various scenarios, we develop a deeper appreciation for the underlying principles that govern mathematical calculations and the consequences of their misinterpretations.
Latest Posts
Latest Posts
-
Balloon Frame Vs Platform Frame
Sep 14, 2025
-
2 5 M En Pied
Sep 14, 2025
-
Purchase Of Supplies On Account
Sep 14, 2025
-
Picture Of A Nervous System
Sep 14, 2025
-
Convertir Des Litres En Ml
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2 1 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.