20 000 Divided By 12
couponhaat
Sep 13, 2025 · 6 min read
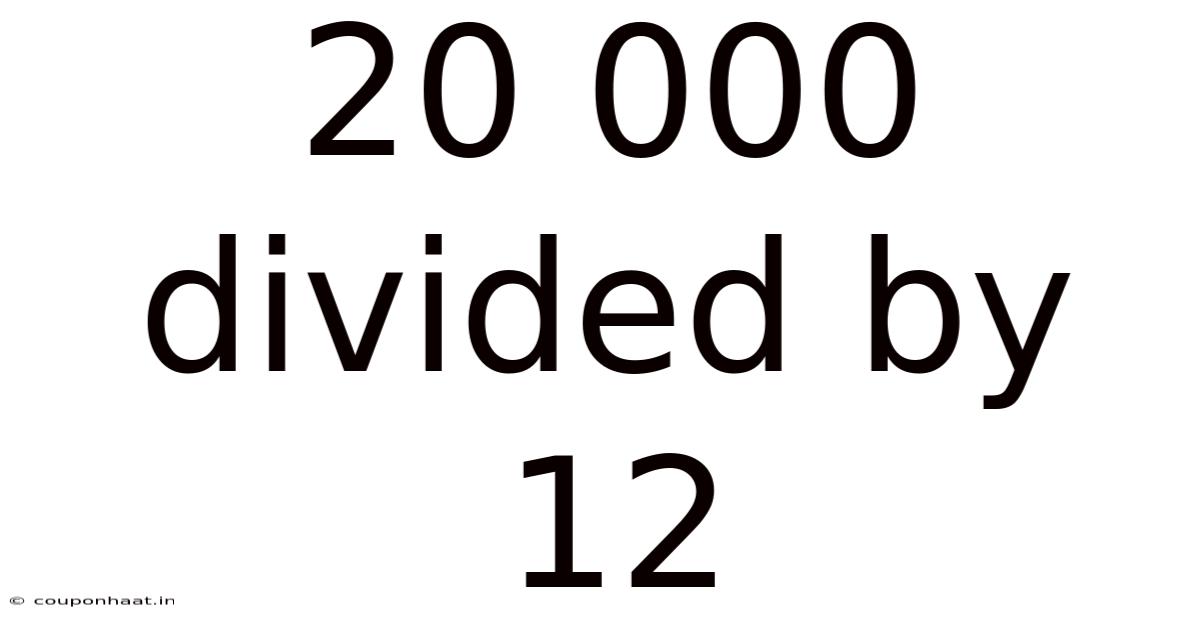
Table of Contents
Unpacking 20,000 Divided by 12: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 20,000 divided by 12, delving far beyond the immediate answer. We'll examine the process of long division, explore different methods for solving this problem, discuss its practical applications in various fields, and address common misconceptions about division. This comprehensive guide is designed for anyone looking to understand this calculation thoroughly, from elementary school students to adults seeking to refresh their mathematical skills. By the end, you’ll not only know the answer but also grasp the underlying concepts and practical implications of this fundamental arithmetic operation.
Understanding the Problem: 20,000 ÷ 12
The problem, 20,000 divided by 12 (or 20,000 ÷ 12), asks: how many times does 12 fit into 20,000? This is a classic division problem, where 20,000 is the dividend (the number being divided) and 12 is the divisor (the number we're dividing by). The result is called the quotient. We'll also often encounter a remainder, which is the amount left over if the division isn't perfectly even.
Method 1: Long Division – The Traditional Approach
Long division is a fundamental arithmetic method taught in schools. It's a systematic way to break down the division problem into manageable steps. Let's work through 20,000 ÷ 12 using long division:
-
Set up the problem: Write 20,000 inside the long division symbol (⟌) and 12 outside.
-
Divide the first digits: 12 doesn't go into 2, so we consider the first three digits: 200. How many times does 12 go into 200? It goes in 16 times (12 x 16 = 192). Write 16 above the 00.
-
Multiply and subtract: Multiply 16 by 12 (192) and write it below 200. Subtract 192 from 200, leaving a remainder of 8.
-
Bring down the next digit: Bring down the next digit (0) from the dividend, making the new number 80.
-
Repeat steps 2-4: How many times does 12 go into 80? It goes in 6 times (12 x 6 = 72). Write 6 above the next 0. Subtract 72 from 80, leaving a remainder of 8.
-
Bring down the last digit: Bring down the last 0, making the new number 80.
-
Repeat steps 2-4: Again, 12 goes into 80 six times (72). Subtract 72 from 80, leaving a remainder of 8.
Therefore, 20,000 divided by 12 is 1666 with a remainder of 8. We can express this as 1666 R8 or as a mixed number: 1666 ⁸⁄₁₂ (which simplifies to 1666 ⅔).
Method 2: Using a Calculator
The simplest method, especially for larger numbers, is to use a calculator. Simply input 20000 ÷ 12 and the calculator will provide the answer, usually as a decimal: 1666.666666... This decimal representation is equivalent to the mixed number 1666 ⅔ we obtained using long division.
Method 3: Breaking Down the Problem
We can also solve this problem by breaking it down. We know that 12 x 1000 = 12,000. This leaves 8000. Then, we can estimate how many times 12 goes into 8000. A rough estimate is 666 (12 x 666 = 7992), leaving a remainder of 8. Adding this to our initial 1000, we get 1666 with a remainder of 8. This method demonstrates a practical approach to estimation and approximation, valuable when dealing with large numbers or situations where exactness is not strictly required.
Real-World Applications of Division Problems like 20,000 ÷ 12
Division is a fundamental operation used across many fields. Here are a few examples where a problem similar to 20,000 ÷ 12 might arise:
-
Finance: Imagine you have $20,000 to invest in 12 equal monthly installments. Dividing 20,000 by 12 helps determine the amount of each installment.
-
Manufacturing: If a factory produces 20,000 units of a product over 12 months, dividing 20,000 by 12 calculates the average monthly production.
-
Project Management: If a project requires 20,000 hours of work and is to be completed over 12 months, the division helps determine the average number of hours required per month.
-
Resource Allocation: Distributing 20,000 resources (like books, supplies, or personnel) among 12 different locations requires the division to determine the allocation per location.
-
Data Analysis: Analyzing datasets often involves dividing a total count (20,000) by a number of categories (12) to calculate averages or proportions.
Understanding Remainders and Decimals
The remainder of 8 in our problem highlights the importance of understanding how division works. The remainder indicates that 12 doesn't perfectly divide into 20,000. We can express the result as a fraction (⁸⁄₁₂ which simplifies to ⅔) or a decimal (0.666...). The decimal representation often continues infinitely, represented by the ellipsis (...). The choice between using a remainder, a fraction, or a decimal depends on the context and the level of precision required.
Frequently Asked Questions (FAQs)
Q1: Why is long division important even in the age of calculators?
A1: Long division helps build a strong foundation in understanding the concept of division. It teaches you the underlying principles, making you less reliant on technology and improving your number sense. It also helps you grasp the concept of remainders and their implications.
Q2: What if the divisor is a larger number?
A2: The process of long division remains the same. The steps may be longer and more complex, but the underlying principles are consistent.
Q3: Can I use different methods to solve division problems?
A3: Absolutely. Using alternative methods like breaking down the problem or using estimation can be helpful, especially for mental calculations or quick approximations. Calculators are also invaluable tools, particularly for complex problems.
Q4: How do I handle a decimal divisor?
A4: When dealing with decimal divisors, you usually want to convert the divisor to a whole number by multiplying both the dividend and the divisor by a power of 10 (e.g., multiplying by 10, 100, 1000, etc., to shift the decimal point). This simplifies the division process.
Conclusion: Beyond the Answer – Mastering Division
This article demonstrates that solving 20,000 divided by 12 goes beyond simply getting the answer (1666 with a remainder of 8 or 1666.666...). Understanding the various methods, the underlying principles of division, and the practical applications of this fundamental operation is crucial for developing strong mathematical skills. Whether you're a student learning arithmetic or an adult seeking to improve your numerical abilities, mastering division lays a solid foundation for tackling more complex mathematical concepts and real-world problems. The ability to not just calculate but also to comprehend the meaning and context behind the numbers is what truly distinguishes mathematical proficiency. Remember to always consider the context of the problem to determine the most appropriate way to represent your answer—as a whole number with a remainder, a fraction, or a decimal.
Latest Posts
Related Post
Thank you for visiting our website which covers about 20 000 Divided By 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.