3/4 Tasse Divisé Par 2
couponhaat
Sep 16, 2025 · 5 min read
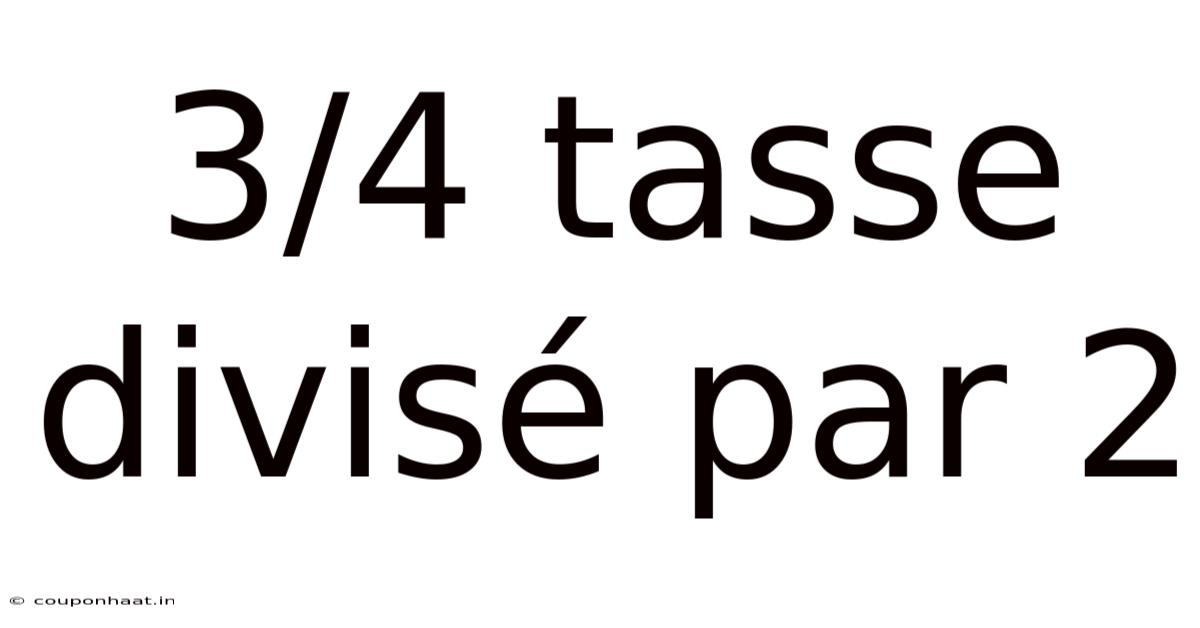
Table of Contents
3/4 of a Cup Divided by 2: A Comprehensive Guide to Fraction Division
Understanding fractions is a cornerstone of mathematics, crucial for various applications from baking to advanced physics. This article will delve into the seemingly simple problem of dividing 3/4 of a cup by 2, exploring not only the solution but also the underlying principles and practical applications. We'll break down the process step-by-step, explaining the mathematical concepts involved and answering frequently asked questions. This guide is designed for anyone looking to solidify their understanding of fraction division, regardless of their prior mathematical experience.
Understanding the Problem: 3/4 Cup ÷ 2
The problem "3/4 of a cup divided by 2" asks us to determine the size of each portion if we divide 3/4 of a cup into two equal parts. This involves dividing a fraction (3/4) by a whole number (2). At first glance, this might seem daunting, but with a clear understanding of the process, it becomes straightforward.
Step-by-Step Solution
We can approach this problem in two main ways:
Method 1: Using the Reciprocal
This method involves converting the division problem into a multiplication problem using the reciprocal. The reciprocal of a number is simply 1 divided by that number. For example, the reciprocal of 2 is 1/2.
-
Rewrite the problem: Instead of 3/4 ÷ 2, we rewrite it as 3/4 × (1/2). Notice that we've replaced the division symbol (÷) with a multiplication symbol (×) and replaced 2 with its reciprocal, 1/2.
-
Multiply the numerators: Multiply the top numbers (numerators) together: 3 × 1 = 3.
-
Multiply the denominators: Multiply the bottom numbers (denominators) together: 4 × 2 = 8.
-
Simplify the fraction: Our result is 3/8. This fraction is already in its simplest form, as 3 and 8 share no common factors other than 1.
Therefore, 3/4 of a cup divided by 2 is equal to 3/8 of a cup.
Method 2: Dividing the Numerator
This method is a shortcut applicable when dividing a fraction by a whole number.
-
Keep the denominator: The denominator (the bottom number) of the fraction remains unchanged. In our case, the denominator stays as 8.
-
Divide the numerator: Divide the numerator (the top number) by the whole number: 3 ÷ 2 = 1.5.
-
Form the new fraction: The resulting fraction is 1.5/4. While this is a correct answer, it's often preferable to express fractions as proper fractions or mixed numbers.
-
Convert to a proper fraction: To convert 1.5/4 to a proper fraction, we can multiply both the numerator and denominator by 2 to eliminate the decimal: (1.5 × 2) / (4 × 2) = 3/8.
This again gives us the answer of 3/8 of a cup.
Visualizing the Solution
Imagine a measuring cup divided into four equal parts. 3/4 of a cup represents three of these four parts. To divide this amount by 2, we're essentially splitting those three parts into two equal groups. Each group would then contain 1.5 parts out of the original four, or 3/8 of the cup. This visual representation reinforces the mathematical solution.
The Importance of Understanding Fraction Division
The ability to divide fractions is essential in numerous contexts:
-
Cooking and Baking: Recipes often require precise measurements. Dividing fractions allows you to adjust recipes to serve fewer people or to use different sized containers.
-
Construction and Engineering: Precise measurements and calculations are critical in construction and engineering projects. Dividing fractions helps in calculating materials, dimensions, and proportions.
-
Data Analysis: In statistics and data analysis, understanding fractions is vital for interpreting percentages, proportions, and ratios.
-
Everyday Life: Even in everyday scenarios, such as sharing snacks or splitting bills, a solid grasp of fraction division is beneficial.
Further Exploration: Dividing Fractions by Fractions
While this article focuses on dividing a fraction by a whole number, the principles can be extended to dividing a fraction by another fraction. To do this, you would again utilize the reciprocal method.
For example, to solve 3/4 ÷ 1/2:
-
Rewrite as multiplication: 3/4 × 2/1 (the reciprocal of 1/2 is 2/1)
-
Multiply numerators and denominators: (3 × 2) / (4 × 1) = 6/4
-
Simplify: 6/4 simplifies to 3/2 or 1 ½
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, most calculators can handle fraction division. However, understanding the underlying mathematical principles is crucial for problem-solving and for situations where a calculator might not be readily available.
Q: What if I'm dividing 3/4 of a cup by a fraction, not a whole number?
A: Follow the same reciprocal method as described above. Remember to always multiply by the reciprocal of the divisor (the number you're dividing by).
Q: Why is the reciprocal method used?
A: The reciprocal method is used because division by a fraction is equivalent to multiplying by its reciprocal. This is a fundamental property of fractions that simplifies the calculation process.
Q: Are there other ways to solve this problem?
A: While the reciprocal method and dividing the numerator are the most common and efficient methods, you could also visualize the problem using diagrams or models to understand the solution.
Conclusion
Dividing 3/4 of a cup by 2 results in 3/8 of a cup. This seemingly simple problem highlights the importance of understanding fraction division, a fundamental skill applicable in diverse fields and everyday situations. By mastering this concept, you'll build a stronger foundation in mathematics and improve your ability to tackle more complex problems involving fractions. Remember to practice regularly, utilize different methods, and visualize the problem to enhance your comprehension and build confidence in your mathematical abilities. The key takeaway is not just the answer itself, but the understanding of the process and the ability to apply it to similar problems.
Latest Posts
Latest Posts
-
Color Wheel And Mixing Colors
Sep 16, 2025
-
Quasimodo Predicted All Of This
Sep 16, 2025
-
What Is 75f In Centigrade
Sep 16, 2025
-
Number Of Protons In Krypton
Sep 16, 2025
-
Mom And Son Role Play
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Tasse Divisé Par 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.