44 50 As A Percentage
couponhaat
Sep 15, 2025 · 5 min read
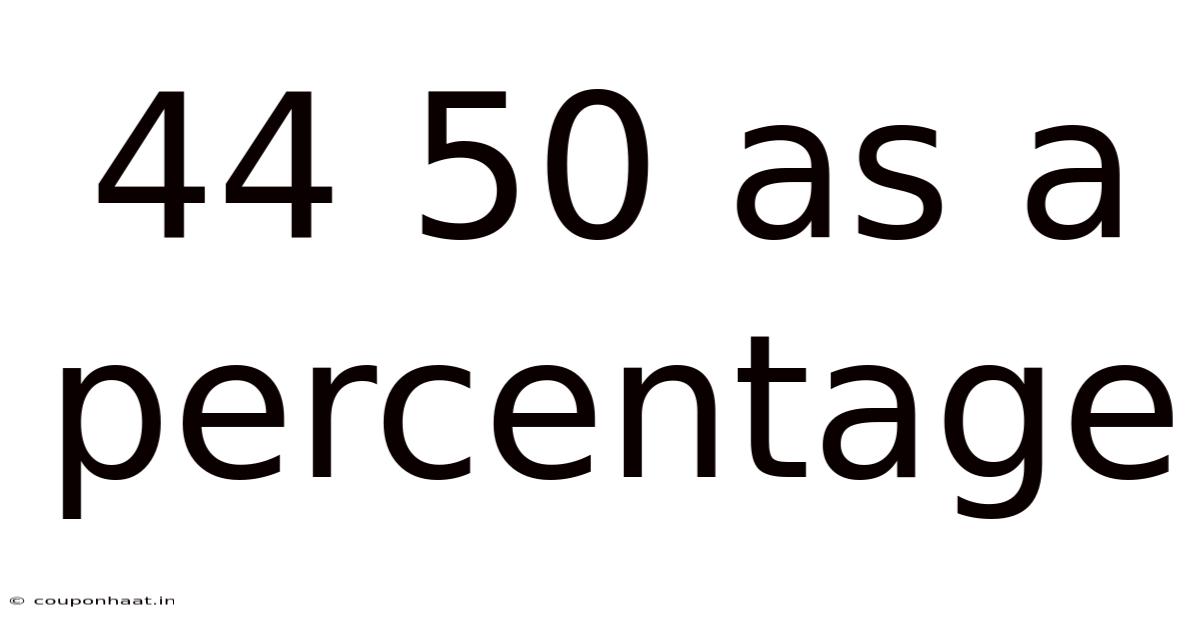
Table of Contents
Decoding the Percentage: Understanding 44/50 as a Percentage
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analysis. This comprehensive guide delves into the calculation and interpretation of 44/50 as a percentage, providing a detailed explanation suitable for all levels of understanding. We'll explore the process step-by-step, discuss the underlying mathematical principles, and offer real-world examples to solidify your comprehension. By the end, you'll not only know how to calculate 44/50 as a percentage but also understand the broader implications of percentage calculations.
Understanding Fractions and Percentages
Before diving into the specific calculation, let's establish a clear understanding of the fundamental concepts: fractions and percentages. A fraction represents a part of a whole. In the case of 44/50, 44 represents the part and 50 represents the whole. A percentage, denoted by the symbol %, expresses a fraction as a portion of 100. Essentially, a percentage is a specific type of fraction where the denominator is always 100.
Calculating 44/50 as a Percentage: A Step-by-Step Guide
The process of converting a fraction to a percentage involves two straightforward steps:
Step 1: Convert the fraction to a decimal.
To do this, we divide the numerator (the top number) by the denominator (the bottom number):
44 ÷ 50 = 0.88
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
0.88 × 100 = 88%
Therefore, 44/50 is equal to 88%.
Different Methods for Calculating Percentages
While the above method is the most straightforward, several alternative approaches can be used to calculate percentages, especially when dealing with more complex fractions or when mental calculations are preferred.
Method 1: Using Proportions
This method leverages the concept of equivalent ratios. We can set up a proportion:
44/50 = x/100
To solve for 'x' (the percentage), we cross-multiply:
50x = 4400
x = 4400 ÷ 50 = 88
Therefore, x = 88%, confirming our previous result.
Method 2: Using the Percentage Formula
The percentage formula provides a more generalized approach:
Percentage = (Part / Whole) × 100
In our case:
Percentage = (44 / 50) × 100 = 88%
This formula is particularly useful when dealing with various scenarios involving parts and wholes.
Real-World Applications of Percentage Calculations: Examples
Understanding percentages is crucial for navigating various aspects of daily life and professional settings. Here are a few illustrative examples:
-
Academic Performance: If a student answers 44 out of 50 questions correctly on a test, their score is 88%. This percentage provides a clear indication of their performance relative to the total possible score.
-
Sales and Discounts: A store offering an 88% discount on an item means the customer pays only 12% of the original price. Understanding percentages is vital for evaluating the actual savings.
-
Financial Calculations: Interest rates, investment returns, and tax calculations all rely heavily on percentage calculations. For example, an annual interest rate of 88% on a loan signifies a significant cost.
-
Data Analysis: Percentages are frequently used in data analysis to represent proportions and trends. For instance, in market research, 88% market share indicates a dominant position.
-
Scientific Studies: Percentage calculations are integral to statistical analysis in scientific research, allowing researchers to present and interpret their findings accurately.
Beyond the Basics: Understanding the Implications of 88%
While the calculation of 44/50 as 88% is straightforward, understanding the context and implications of this percentage is crucial. An 88% score on a test, for example, suggests a high level of mastery, whereas an 88% market share demonstrates significant market dominance. The interpretation of the percentage depends entirely on the specific context in which it's used.
Frequently Asked Questions (FAQs)
Q1: How do I calculate percentages in my head quickly?
A1: For quick mental calculations, focus on familiar fractions. For example, knowing that 1/2 = 50%, 1/4 = 25%, and 1/10 = 10% can help you estimate percentages efficiently. You can also round numbers to make calculations simpler.
Q2: What if I have a fraction with a larger denominator?
A2: The same principle applies: divide the numerator by the denominator and multiply the result by 100. The process remains identical, regardless of the size of the numbers.
Q3: Are there any online calculators for percentage calculations?
A3: Yes, numerous online calculators are available to assist with percentage calculations. These tools can be particularly helpful when dealing with complex calculations or large numbers. However, understanding the underlying process remains beneficial for problem-solving and critical thinking.
Q4: How can I improve my understanding of percentages?
A4: Practice is key! Work through various examples, try different methods, and apply percentage calculations to real-world scenarios. This hands-on approach will solidify your understanding and build your confidence.
Conclusion: Mastering Percentage Calculations
Calculating 44/50 as a percentage—resulting in 88%—is a fundamental skill with wide-ranging applications. This guide has not only provided a step-by-step approach to this specific calculation but has also explored broader concepts related to fractions, decimals, and percentages. By understanding the underlying principles and practicing various methods, you can confidently tackle percentage calculations in any context, fostering greater numerical literacy and problem-solving abilities. Remember that the power of percentages lies not just in the calculation itself but in its ability to provide meaningful insights and inform decisions across diverse fields. Continual practice and application will solidify your understanding and empower you to utilize percentages effectively in your daily life and professional endeavors.
Latest Posts
Latest Posts
-
7 20 As A Percent
Sep 15, 2025
-
Map Of The Pyrenees Mountains
Sep 15, 2025
-
Past Tense Verbs In Spanish
Sep 15, 2025
-
Ruler Of Millimeters Actual Size
Sep 15, 2025
-
Johann Wyss Swiss Family Robinson
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 44 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.