Cos 2 Sin 2 1
couponhaat
Sep 13, 2025 · 5 min read
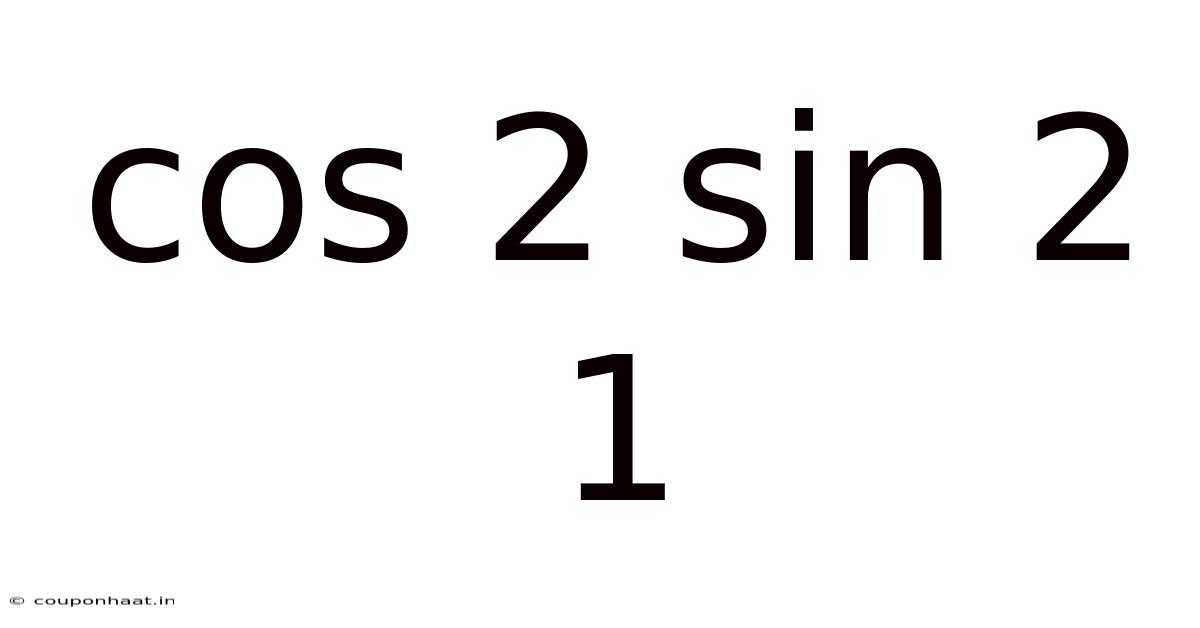
Table of Contents
Decoding cos²θ - sin²θ = 1: A Deep Dive into Trigonometric Identities
This article explores the trigonometric identity cos²θ - sin²θ = 1, examining its derivation, applications, and connections to other fundamental trigonometric relationships. While the equation as stated is incorrect (the correct form involves a plus sign, not a minus), we will delve into the correct identity, cos²θ + sin²θ = 1, and explore its implications and related identities. Understanding this core identity is crucial for mastering trigonometry and its applications in various fields like physics, engineering, and computer graphics.
Introduction: The Pythagorean Identity
The equation cos²θ + sin²θ = 1 is known as the Pythagorean identity. It's a fundamental relationship between the sine and cosine functions of an angle θ. This identity stems directly from the Pythagorean theorem in geometry, and its proof provides a clear link between trigonometry and geometry.
Geometric Proof of cos²θ + sin²θ = 1
Imagine a right-angled triangle with hypotenuse of length 1. Let θ be one of the acute angles. The side adjacent to θ has length cos θ, and the side opposite to θ has length sin θ. By the Pythagorean theorem, the square of the hypotenuse equals the sum of the squares of the other two sides:
1² = (cos θ)² + (sin θ)²
This simplifies to:
cos²θ + sin²θ = 1
This geometric proof provides an intuitive understanding of the identity. It works for any acute angle θ. However, the identity holds true for all angles, not just acute angles, as we'll see in the next section.
Extending the Proof to All Angles
The geometric proof works beautifully for acute angles. But what about obtuse angles, or even negative angles? To extend the proof to all angles, we need to consider the unit circle.
The unit circle is a circle with a radius of 1 centered at the origin of a coordinate system. Any point on the unit circle can be represented by its coordinates (x, y), where x = cos θ and y = sin θ, and θ is the angle formed by the positive x-axis and the line segment connecting the origin to the point (x, y).
From the equation of a circle, we know that x² + y² = r², where r is the radius. Since we are on the unit circle, r = 1. Substituting x = cos θ and y = sin θ, we get:
(cos θ)² + (sin θ)² = 1²
cos²θ + sin²θ = 1
This derivation holds for any angle θ, regardless of its quadrant or sign. The unit circle approach neatly handles all possible angles, thus confirming the universality of the Pythagorean identity.
Applications of the Pythagorean Identity
The Pythagorean identity is not just a theoretical result; it's a powerful tool used extensively in various areas:
-
Simplifying Trigonometric Expressions: The identity allows us to simplify complex expressions by replacing cos²θ or sin²θ with their equivalents in terms of the other function. For example, an expression containing sin⁴θ can be simplified using the identity repeatedly.
-
Solving Trigonometric Equations: Many trigonometric equations can be simplified and solved more easily using the Pythagorean identity. This often involves substituting one trigonometric function with its equivalent expression derived from the identity.
-
Calculus: The Pythagorean identity plays a vital role in various calculus techniques, particularly in integration and differentiation of trigonometric functions. It helps in simplifying integrands and reducing complex expressions.
-
Physics and Engineering: In fields like physics and engineering, the Pythagorean identity is crucial in analyzing oscillatory motion, wave phenomena, and AC circuits. It's instrumental in resolving vectors and simplifying equations related to these phenomena.
Deriving Other Trigonometric Identities
The Pythagorean identity is a cornerstone from which many other important trigonometric identities can be derived. For instance:
-
tan²θ + 1 = sec²θ: Dividing the Pythagorean identity by cos²θ gives us this identity, relating tangent and secant functions.
-
1 + cot²θ = csc²θ: Similarly, dividing the Pythagorean identity by sin²θ yields this identity, connecting cotangent and cosecant functions.
These derived identities are just as crucial as the Pythagorean identity itself in solving trigonometric problems and simplifying complex expressions.
Working with the Pythagorean Identity: Examples
Let's look at a few examples showcasing the utility of the Pythagorean identity:
Example 1: Simplifying an expression
Simplify the expression: sin⁴θ + 2sin²θcos²θ + cos⁴θ
We can rewrite the expression as (sin²θ + cos²θ)² Since sin²θ + cos²θ = 1, the entire expression simplifies to 1².
Example 2: Solving a trigonometric equation
Solve for θ: 2cos²θ - 1 = 0
Using the Pythagorean identity, we can replace cos²θ with 1 - sin²θ:
2(1 - sin²θ) - 1 = 0
Solving this quadratic equation for sin θ and then finding the corresponding values of θ provides the solution.
Example 3: Calculus application
Consider the integral: ∫sin²θ dθ. We can use the identity cos²θ = 1 - sin²θ to rewrite the integral and solve it more easily.
Frequently Asked Questions (FAQ)
Q1: Why is the Pythagorean identity so important?
A1: The Pythagorean identity is fundamental because it establishes a crucial relationship between the sine and cosine functions. This relationship simplifies complex trigonometric expressions, solves equations, and underlies many other identities and applications in various scientific and engineering fields.
Q2: Is the Pythagorean identity only valid for right-angled triangles?
A2: While initially derived using a right-angled triangle, its validity extends beyond right-angled triangles. The unit circle approach demonstrates its validity for all angles.
Q3: How can I remember the Pythagorean identity?
A3: Visualizing the unit circle and recalling the Pythagorean theorem in geometry are helpful memory aids. The identity is straightforward; the sum of the squares of cosine and sine always equals 1.
Q4: What are some common mistakes students make when using this identity?
A4: Common errors include: forgetting the identity entirely, misusing the plus sign (using a minus sign instead), and incorrectly applying it to simplify expressions. Careful attention to detail and practice are key to avoiding these mistakes.
Conclusion: The Power of a Fundamental Identity
The Pythagorean identity, cos²θ + sin²θ = 1, stands as a cornerstone of trigonometry. Its geometric foundation and its elegant extension to all angles using the unit circle demonstrate its power and universality. This identity is not just a theoretical result; it's a practical tool used constantly to simplify expressions, solve equations, and tackle problems in various fields. Mastering this identity and its applications is essential for anyone pursuing further studies in mathematics, science, or engineering. By understanding its derivation, applications, and relationship to other trigonometric identities, you will have a solid foundation to build upon your trigonometric knowledge. Remember to practice regularly and to fully appreciate the elegance and utility of this fundamental mathematical relationship.
Latest Posts
Latest Posts
-
French Words Beginning With L
Sep 13, 2025
-
Lewis Structure For Magnesium Chloride
Sep 13, 2025
-
British Gallon Vs Us Gallon
Sep 13, 2025
-
Difference Between Prejudice And Stereotype
Sep 13, 2025
-
Is A Cylinder A Prism
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Cos 2 Sin 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.