Derivative Of X 2e X
couponhaat
Sep 13, 2025 · 6 min read
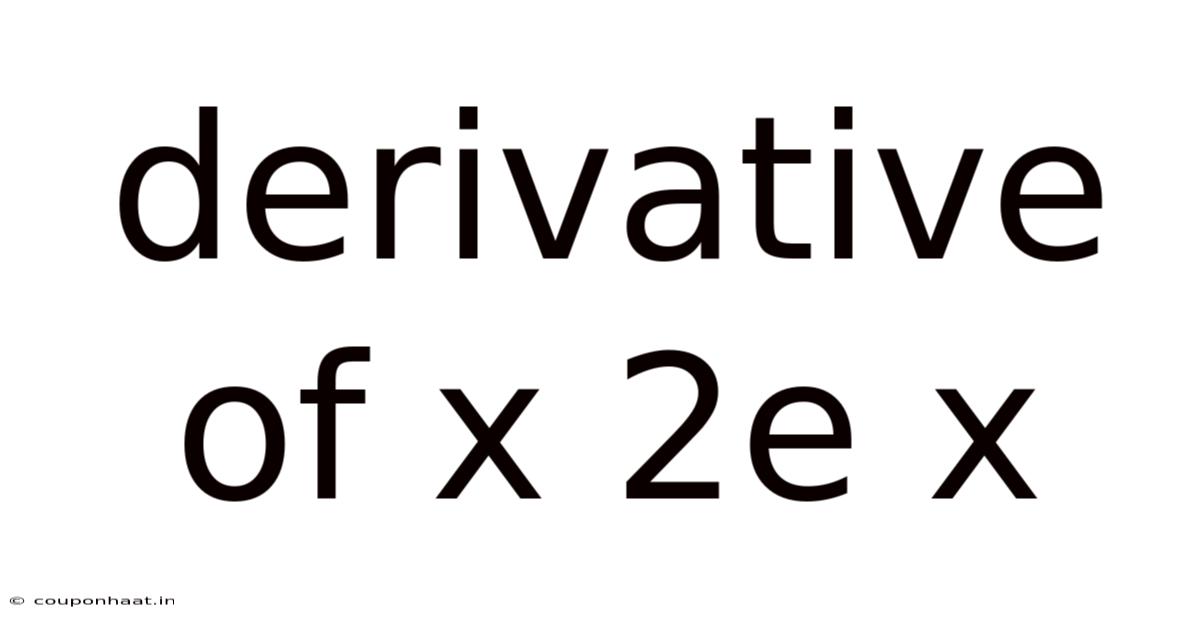
Table of Contents
Demystifying the Derivative of x²eˣ: A Comprehensive Guide
Finding the derivative of functions is a cornerstone of calculus, crucial for understanding rates of change and optimization problems. This article delves into the derivation of the function f(x) = x²eˣ, providing a step-by-step explanation, exploring the underlying rules of calculus, and addressing common questions. We will cover the product rule, exponential derivatives, and provide a deeper understanding of this specific derivative, making it accessible to students of various mathematical backgrounds.
Introduction: Understanding the Components
Before tackling the derivative of x²eˣ, let's review the essential components: x², eˣ, and the product rule.
-
x²: This is a simple power function. Its derivative is found using the power rule: d/dx (xⁿ) = nxⁿ⁻¹. Therefore, the derivative of x² is 2x.
-
eˣ: This is the exponential function with base e (Euler's number, approximately 2.718). The remarkable property of eˣ is that its derivative is itself: d/dx (eˣ) = eˣ. This is a fundamental result in calculus.
-
The Product Rule: Since our function is a product of two functions (x² and eˣ), we need the product rule to find its derivative. The product rule states that if we have a function h(x) = f(x)g(x), then its derivative is h'(x) = f'(x)g(x) + f(x)g'(x).
Step-by-Step Derivation: Applying the Product Rule
Now, let's apply the product rule to find the derivative of f(x) = x²eˣ.
-
Identify f(x) and g(x): In our function, let f(x) = x² and g(x) = eˣ.
-
Find the derivatives f'(x) and g'(x):
- f'(x) = d/dx (x²) = 2x (using the power rule)
- g'(x) = d/dx (eˣ) = eˣ (using the derivative of eˣ)
-
Apply the product rule: Substitute f(x), g(x), f'(x), and g'(x) into the product rule formula:
f'(x) = f'(x)g(x) + f(x)g'(x) = (2x)(eˣ) + (x²)(eˣ)
-
Simplify the expression: We can factor out eˣ to simplify the result:
f'(x) = eˣ(2x + x²)
Therefore, the derivative of x²eˣ is eˣ(2x + x²).
Understanding the Result: A Deeper Dive
The derivative, eˣ(2x + x²), represents the instantaneous rate of change of the function x²eˣ at any given point x. Let's analyze this result further:
-
The exponential factor (eˣ): The presence of eˣ indicates that the rate of change is always influenced by exponential growth. As x increases, the rate of change increases exponentially.
-
The polynomial factor (2x + x²): This quadratic term modifies the exponential growth. For negative values of x, the polynomial factor can be negative, but the exponential factor is always positive. The interplay between these two factors determines the overall behavior of the derivative.
-
Critical Points: To find critical points (where the derivative is zero or undefined), we set the derivative equal to zero:
eˣ(2x + x²) = 0
Since eˣ is never zero, we only need to solve the quadratic equation:
2x + x² = 0
x(2 + x) = 0
This gives us two critical points: x = 0 and x = -2. These points represent potential local minima or maxima of the original function f(x) = x²eˣ.
Graphical Representation and Interpretation
Plotting both f(x) = x²eˣ and its derivative f'(x) = eˣ(2x + x²) provides a visual understanding of their relationship. The graph of f(x) shows an increasing function that approaches zero as x approaches negative infinity and increases rapidly as x becomes positive. The graph of f'(x) shows where the function f(x) is increasing (f'(x) > 0) and decreasing (f'(x) < 0). The points where f'(x) = 0 correspond to the critical points of f(x).
Higher-Order Derivatives
We can also find higher-order derivatives of x²eˣ. For instance, the second derivative represents the rate of change of the rate of change. Let's find the second derivative:
-
Start with the first derivative: f'(x) = eˣ(2x + x²)
-
Apply the product rule again: This time, let f(x) = eˣ and g(x) = (2x + x²). Then f'(x) = eˣ and g'(x) = 2 + 2x.
-
Applying the product rule: f''(x) = f'(x)g(x) + f(x)g'(x) = eˣ(2x + x²) + eˣ(2 + 2x)
-
Simplify: f''(x) = eˣ(x² + 4x + 2)
The second derivative, eˣ(x² + 4x + 2), provides information about the concavity of the original function.
Applications in Science and Engineering
The derivative of x²eˣ and similar functions have widespread applications in various fields:
-
Physics: Modeling exponential growth or decay processes, such as radioactive decay or population growth, often involves functions of this form. The derivative helps determine the rate of these processes.
-
Engineering: Analyzing systems with exponential responses, such as electrical circuits or mechanical systems with damping, utilizes derivatives to understand transient behavior.
-
Economics and Finance: In financial modeling, exponential functions are used to describe compound interest and growth of investments. Derivatives help analyze the rate of return and optimal investment strategies.
-
Probability and Statistics: In probability distributions like the normal distribution, exponential functions are crucial components. Derivatives are used in calculating probabilities and statistical measures.
Frequently Asked Questions (FAQ)
Q1: What if the function was x³eˣ instead of x²eˣ? How would the derivative change?
A1: The process remains the same, but with a slightly different outcome. You would still use the product rule. Let f(x) = x³ and g(x) = eˣ. Then f'(x) = 3x² and g'(x) = eˣ. Applying the product rule, the derivative of x³eˣ would be eˣ(3x² + x³).
Q2: Can we use the chain rule for this problem?
A2: No, the chain rule is not directly applicable here. The chain rule is used for composite functions (functions within functions). This function is a product of two separate functions, making the product rule the appropriate technique.
Q3: How do I find the integral of x²eˣ?
A3: Finding the integral of x²eˣ requires integration by parts, a more advanced technique than differentiation. It involves repeatedly applying the integration by parts formula.
Conclusion: Mastering the Fundamentals
Understanding the derivative of x²eˣ is not just about memorizing a formula; it's about understanding the fundamental concepts of calculus, such as the product rule, derivatives of power functions and exponential functions. By breaking down the problem into manageable steps and understanding the underlying principles, you can confidently tackle more complex derivative problems and appreciate the power of calculus in analyzing real-world phenomena. This detailed explanation provides a solid foundation for further exploration into the fascinating world of calculus and its applications. Remember to practice regularly, and you'll master this valuable skill in no time.
Latest Posts
Latest Posts
-
Number Of Protons In Li
Sep 13, 2025
-
Names For Tree Of Life
Sep 13, 2025
-
Wild Wild West Hotel Vegas
Sep 13, 2025
-
Le Monde Selon Garp Resume
Sep 13, 2025
-
Les Continent Et Les Oceans
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of X 2e X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.