Divide 3 By 1 3
couponhaat
Sep 15, 2025 · 5 min read
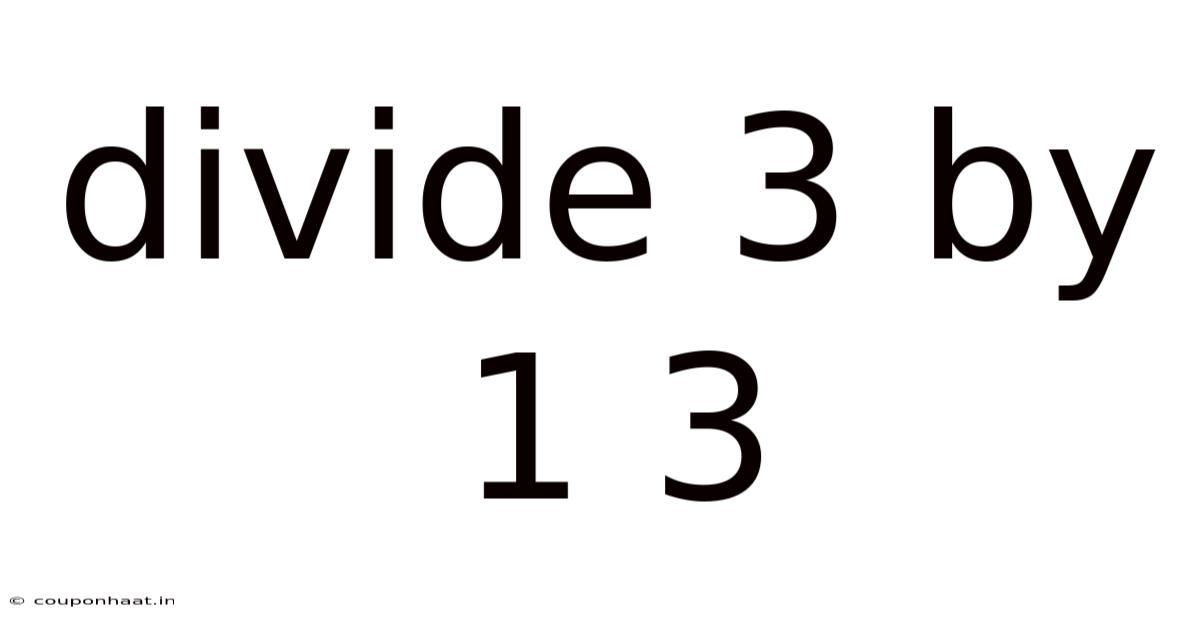
Table of Contents
Diving Deep into 3 ÷ 1⅓: A Comprehensive Exploration of Division with Fractions
Dividing 3 by 1⅓ might seem like a simple arithmetic problem, but it opens the door to a deeper understanding of fractions, division, and their interconnectedness. This article will guide you through the process, exploring multiple methods for solving this problem and expanding on the underlying mathematical concepts. We'll also address common misconceptions and frequently asked questions, leaving you with a solid grasp of how to handle similar division problems involving fractions and mixed numbers.
Understanding the Problem: 3 ÷ 1⅓
Before diving into the solutions, let's clearly define the problem: We need to find out how many times 1⅓ goes into 3. This involves understanding both the dividend (3) and the divisor (1⅓). The dividend is the number being divided, and the divisor is the number we're dividing by. In this case, we're essentially asking: "How many groups of 1⅓ can we make from 3?"
Method 1: Converting to Improper Fractions
This is arguably the most common and straightforward method. It involves converting the mixed number (1⅓) into an improper fraction. Remember, a mixed number combines a whole number and a fraction.
-
Step 1: Convert 1⅓ to an improper fraction. To do this, we multiply the whole number (1) by the denominator (3) and add the numerator (1). This sum (1*3 + 1 = 4) becomes the new numerator, while the denominator remains the same (3). Therefore, 1⅓ is equivalent to ⁴⁄₃.
-
Step 2: Rewrite the division problem. Our problem now becomes 3 ÷ ⁴⁄₃.
-
Step 3: Reciprocal and Multiplication. Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of ⁴⁄₃ is ³⁄₄. So, we change the division problem to a multiplication problem: 3 x ³⁄₄.
-
Step 4: Simplify and Solve. We can write 3 as ³⁄₁. Now we multiply the numerators together (3 x 3 = 9) and the denominators together (1 x 4 = 4). This gives us ⁹⁄₄.
-
Step 5: Convert back to a mixed number (optional). ⁹⁄₄ is an improper fraction. To convert it to a mixed number, we divide the numerator (9) by the denominator (4). This gives us 2 with a remainder of 1. Therefore, ⁹⁄₄ is equal to 2¼.
Therefore, 3 ÷ 1⅓ = 2¼
Method 2: Using Decimal Representation
This method involves converting both the dividend and the divisor into decimals.
-
Step 1: Convert 1⅓ to a decimal. To convert ⅓ to a decimal, we perform the division: 1 ÷ 3 = 0.333... (repeating decimal). Therefore, 1⅓ = 1.333...
-
Step 2: Perform the division. Now we divide 3 by 1.333... Using a calculator, this gives us approximately 2.25.
-
Step 3: Understanding the approximation. Because we're using a repeating decimal (0.333...), the result will be an approximation. The more decimal places we use, the more accurate the result will be.
Therefore, approximately 3 ÷ 1⅓ ≈ 2.25
Method 3: Visual Representation
While less precise for complex problems, visualizing the division can be helpful for understanding the concept. Imagine you have 3 units of something, and you want to divide them into groups of 1⅓ units each.
Imagine dividing three whole pizzas into servings of 1 and ⅓ pizza each. You can easily give out two full servings of 1⅓ pizzas, leaving you with a remainder of ⅓ pizza. This remainder represents the fraction part in our answer of 2¼.
This visual approach helps solidify the intuitive understanding of what division with fractions truly represents: separating a quantity into smaller, fractional parts.
Explanation of the Mathematical Principles
The core mathematical principles behind solving 3 ÷ 1⅓ are based on the properties of fractions and division.
-
Converting Mixed Numbers: The conversion of mixed numbers to improper fractions is crucial. It allows us to apply the rules of fraction arithmetic consistently without dealing with the added complexity of separate whole and fractional parts.
-
Reciprocal in Division: The crucial step of changing division to multiplication by the reciprocal is a fundamental rule in fraction division. This stems from the definition of division: dividing by a number is equivalent to multiplying by its multiplicative inverse (reciprocal).
-
Fraction Multiplication: Multiplying fractions involves multiplying the numerators and the denominators separately. Simplification is often possible before or after this multiplication to reduce the resulting fraction to its lowest terms.
Frequently Asked Questions (FAQ)
-
Why can't I just divide 3 by 1 and then by ⅓ separately? Dividing separately would be incorrect because it doesn't reflect the meaning of the original problem (how many times 1⅓ goes into 3). The divisor is a single unit (1⅓), not two separate parts to be divided individually.
-
What if I get a different answer using a calculator? Slight variations can occur depending on the calculator's rounding mechanisms, especially when dealing with repeating decimals. The methods described above provide more accurate results, especially Method 1 (improper fractions).
-
Can I use this method for other problems with fractions and mixed numbers? Absolutely! The principles of converting to improper fractions, using reciprocals, and simplifying fractions are universally applicable in division problems involving fractions and mixed numbers.
-
What are some real-world applications of dividing with fractions? Many real-world scenarios involve dividing with fractions. For instance, consider dividing ingredients for a recipe or calculating the amount of material needed for a construction project based on fractional measurements. It’s a common problem in baking, sewing, and building projects.
Conclusion:
Dividing 3 by 1⅓ isn't just a simple arithmetic problem; it's a gateway to a deeper understanding of fractions and the art of mathematical manipulation. By understanding the methods outlined – converting to improper fractions, using decimal representation, and even visualizing the problem – you gain a more intuitive and profound understanding of division involving fractions. This knowledge extends beyond simple calculations, proving valuable in various fields and problem-solving situations that demand a thorough understanding of fractional arithmetic. Remember, practice makes perfect! The more you work with these concepts, the more comfortable and confident you'll become. So grab your pencil and paper (or calculator), and tackle some more division problems involving fractions – you've got this!
Latest Posts
Latest Posts
-
125 Degrees Farenheit To Celcius
Sep 16, 2025
-
64 Fl Oz To Ml
Sep 16, 2025
-
Climate Of Atlantic Region Canada
Sep 16, 2025
-
Words To Describe The Ocean
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Divide 3 By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.