Integral Of 1 3 X
couponhaat
Sep 16, 2025 · 6 min read
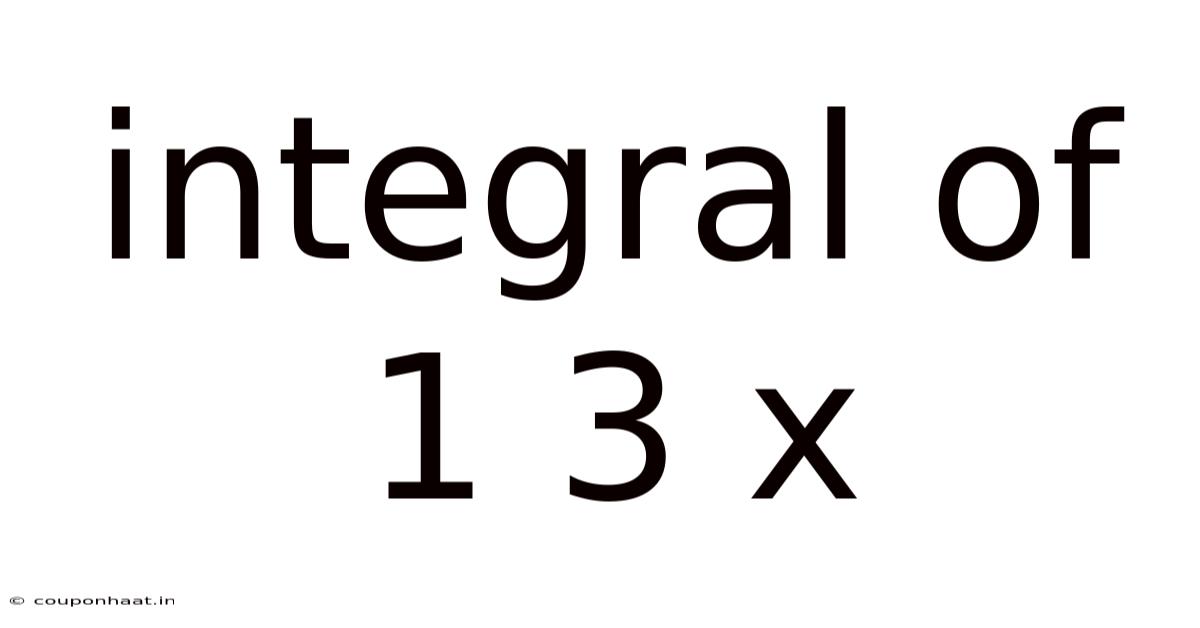
Table of Contents
Understanding and Solving the Integral of 1/(3x)
The integral of 1/(3x) is a fundamental concept in calculus, representing the antiderivative of the function f(x) = 1/(3x). Understanding how to solve this integral is crucial for mastering more complex integration techniques and applications in various fields like physics, engineering, and economics. This article will provide a comprehensive explanation of the process, including the underlying principles and common pitfalls to avoid. We'll delve into the method, explore the constant of integration, and address frequently asked questions.
Introduction: What is an Integral?
Before diving into the specifics of integrating 1/(3x), let's briefly review the concept of integration. Integration is essentially the reverse process of differentiation. While differentiation finds the instantaneous rate of change of a function, integration finds the function whose derivative is the given function. This "original" function is called the antiderivative. The integral of a function f(x) is denoted as ∫f(x)dx. The 'dx' signifies that we are integrating with respect to the variable x.
The integral of 1/(3x) specifically asks: What function, when differentiated, gives us 1/(3x)? This seemingly simple problem introduces important considerations about the domain of the function and the use of absolute values.
Steps to Solve the Integral of 1/(3x)
The key to solving this integral lies in recognizing it as a variation of the integral of 1/x. We can use the property of constants in integration: The integral of a constant times a function is equal to the constant times the integral of the function. Mathematically:
∫cf(x)dx = c∫f(x)dx, where 'c' is a constant.
- Constant Factor: First, we can pull the constant 1/3 out of the integral:
∫(1/(3x))dx = (1/3)∫(1/x)dx
-
Integral of 1/x: The integral of 1/x is a fundamental integral, often memorized as ln|x| + C, where ln represents the natural logarithm and C is the constant of integration. The absolute value is crucial here because the natural logarithm is only defined for positive arguments. Including the absolute value ensures the function's domain encompasses all real numbers except x=0.
-
Combining the Steps: Substituting the integral of 1/x, we obtain:
(1/3)∫(1/x)dx = (1/3)ln|x| + C
Therefore, the integral of 1/(3x) is (1/3)ln|x| + C.
Detailed Explanation and Justification
Let's dissect this solution further. Why is ln|x| the integral of 1/x? The derivative of ln(x) is 1/x, but this is only valid for x > 0. The function ln(x) is undefined for x ≤ 0. To account for negative values of x, we use the absolute value, |x|.
Consider the derivative of ln|x|:
- For x > 0: d/dx[ln(x)] = 1/x
- For x < 0: d/dx[ln(-x)] = (1/(-x)) * (-1) = 1/x (using the chain rule)
In both cases, the derivative is 1/x. This explains why the absolute value is necessary in the antiderivative. The function (1/3)ln|x| + C is the most general antiderivative, encompassing all possible values of x (except x=0, where the original function is undefined).
The Significance of the Constant of Integration (C)
The constant of integration, 'C', is a critical component of the indefinite integral. It represents an arbitrary constant that can take any real value. When we differentiate (1/3)ln|x| + C, the constant C disappears because the derivative of a constant is zero. This means that there is an infinite family of functions whose derivative is 1/(3x), differing only by their vertical shift.
For example:
- (1/3)ln|x| + 1
- (1/3)ln|x| - 5
- (1/3)ln|x| + π
All of these functions have the same derivative: 1/(3x). The specific value of C is determined only if we have additional information, such as a point that the antiderivative must pass through (a boundary condition). This is crucial in definite integration, where we evaluate the integral between specific limits, and the constant cancels out.
Definite Integral of 1/(3x)
If we were dealing with a definite integral, we would evaluate the antiderivative at the upper and lower limits of integration. Let's consider the definite integral from a to b (where a and b are positive):
∫<sub>a</sub><sup>b</sup> (1/(3x)) dx = [(1/3)ln|x|]<sub>a</sub><sup>b</sup> = (1/3)ln|b| - (1/3)ln|a| = (1/3)ln(b/a)
Notice that the constant of integration cancels out in the definite integral.
Common Mistakes and Pitfalls to Avoid
Several common mistakes can occur when solving integrals involving 1/(3x) or similar functions:
-
Forgetting the Absolute Value: Omitting the absolute value signs in ln|x| is a frequent error. Remember, the natural logarithm is only defined for positive arguments.
-
Incorrect Application of the Constant: Incorrectly handling the constant 1/3 during the integration process can lead to errors. Always remember to pull out the constant before integrating.
-
Confusing Integration and Differentiation: It's essential to understand the difference between integration and differentiation. Don't confuse the derivative of ln|x| with its integral.
-
Ignoring the Constant of Integration: Forgetting to add the constant of integration, C, in indefinite integrals is a major mistake that leads to an incomplete solution.
Frequently Asked Questions (FAQ)
Q1: What if the denominator is 3x + k, where k is a constant?
A1: If the denominator is 3x + k, the integral becomes more complex and requires a different technique, such as u-substitution. This is beyond the scope of this explanation focusing on the integral of 1/(3x).
Q2: Can we integrate 1/(3x) using a different method?
A2: While other methods exist for more complex integrals, the method shown above using the known integral of 1/x and the constant multiple rule is the most straightforward and efficient approach for this specific problem.
Q3: What are some real-world applications of this integral?
A3: The integral of 1/x (and its variations) appears frequently in various fields. For instance, in physics, it's involved in calculating work done by a variable force, and in economics, it is used in certain growth models.
Conclusion
The integral of 1/(3x) is (1/3)ln|x| + C. This simple-looking integral underscores the importance of understanding the properties of logarithms, the constant of integration, and the crucial role of the absolute value in ensuring the correct domain for the antiderivative. Mastering this basic integration problem lays a solid foundation for tackling more complex integration problems encountered in various mathematical and scientific disciplines. Remember to always pay close attention to detail and practice regularly to solidify your understanding. By carefully considering the steps and avoiding common pitfalls, you can confidently solve this type of integral and progress to more challenging problems in calculus.
Latest Posts
Latest Posts
-
36 Is How Many Feet
Sep 16, 2025
-
Age Of Consent For Illinois
Sep 16, 2025
-
Unit Of Measurement Of Torque
Sep 16, 2025
-
Refracting Telescope Vs Reflecting Telescope
Sep 16, 2025
-
7 Great Sins In Islam
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 3 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.