Is 3/4 Bigger Than 2/3
couponhaat
Sep 16, 2025 · 6 min read
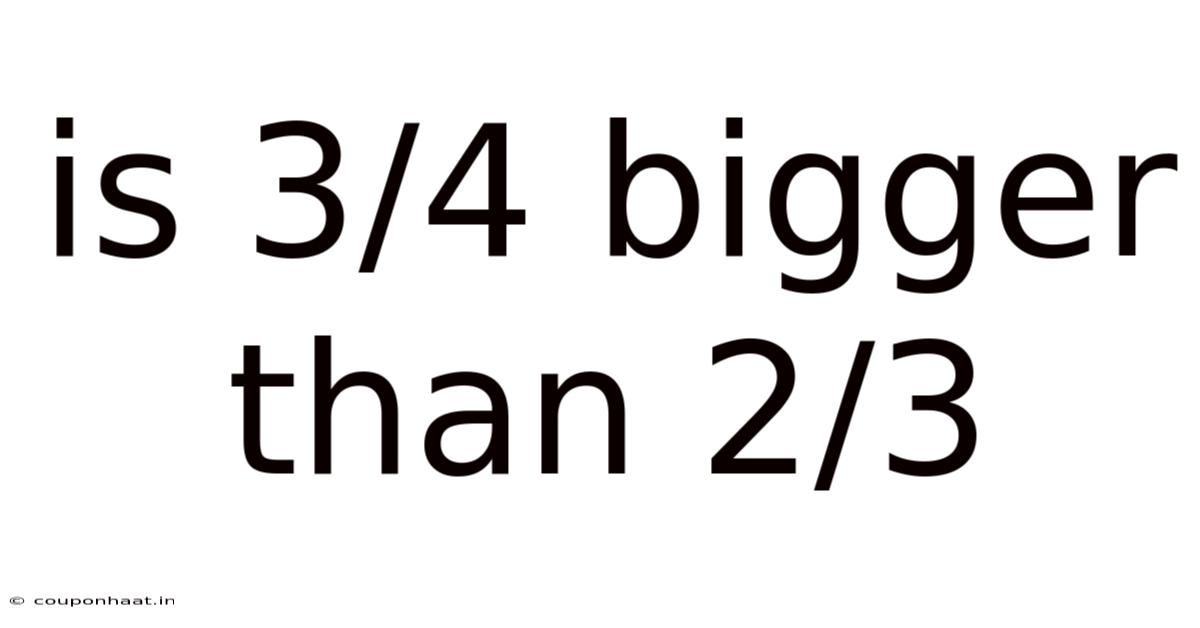
Table of Contents
Is 3/4 Bigger Than 2/3? A Deep Dive into Fraction Comparison
Understanding fractions is fundamental to mathematics, and comparing their relative sizes is a crucial skill. This article will delve into the question: is 3/4 bigger than 2/3? We'll not only answer this specific question but also explore the various methods for comparing fractions, providing a comprehensive understanding for learners of all levels. We'll cover different approaches, from visual representations to numerical calculations, ensuring you can confidently compare any two fractions.
Understanding Fractions: A Quick Recap
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 3/4, the denominator (4) means the whole is divided into four equal parts, and the numerator (3) means we are considering three of those parts.
Method 1: Visual Comparison
A simple and intuitive way to compare fractions is through visual representation. Imagine two identical circles.
- For 3/4: Divide the first circle into four equal parts and shade three of them.
- For 2/3: Divide the second circle into three equal parts and shade two of them.
By visually comparing the shaded areas, it becomes clear that the shaded portion representing 3/4 is larger than the shaded portion representing 2/3. This visual method is particularly helpful for beginners, providing a concrete understanding of fractional magnitudes.
Method 2: Finding a Common Denominator
A more robust method for comparing fractions involves finding a common denominator. This means finding a number that is a multiple of both denominators. Once we have a common denominator, we can directly compare the numerators.
Let's compare 3/4 and 2/3:
-
Find the least common multiple (LCM) of the denominators: The denominators are 4 and 3. The multiples of 4 are 4, 8, 12, 16... The multiples of 3 are 3, 6, 9, 12, 15... The least common multiple is 12.
-
Convert the fractions to equivalent fractions with the common denominator:
- To convert 3/4 to a fraction with a denominator of 12, we multiply both the numerator and the denominator by 3: (3 x 3) / (4 x 3) = 9/12
- To convert 2/3 to a fraction with a denominator of 12, we multiply both the numerator and the denominator by 4: (2 x 4) / (3 x 4) = 8/12
-
Compare the numerators: Now we compare 9/12 and 8/12. Since 9 > 8, we conclude that 9/12 (or 3/4) is greater than 8/12 (or 2/3).
Method 3: Converting to Decimals
Another effective method is converting the fractions to decimals. This allows for a direct numerical comparison.
-
Convert 3/4 to a decimal: Divide the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75
-
Convert 2/3 to a decimal: Divide the numerator (2) by the denominator (3): 2 ÷ 3 ≈ 0.6667 (this is a repeating decimal)
-
Compare the decimals: Since 0.75 > 0.6667, we conclude that 3/4 is greater than 2/3.
Method 4: Cross-Multiplication
Cross-multiplication offers a quick and efficient way to compare fractions.
-
Cross-multiply the fractions: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa.
- 3/4 and 2/3: (3 x 3) = 9 and (4 x 2) = 8
-
Compare the results: The larger product corresponds to the larger fraction. Since 9 > 8, 3/4 is greater than 2/3.
Why Different Methods Matter
While all four methods lead to the same conclusion – 3/4 is bigger than 2/3 – understanding each method is crucial. The visual method provides an intuitive grasp of the concept, particularly for younger learners. The common denominator method builds a strong foundation for more complex fraction operations. Decimal conversion is useful when dealing with calculations involving decimals and percentages. Cross-multiplication offers a quick solution for simple comparisons. Choosing the appropriate method depends on the context and the learner's understanding.
Beyond the Comparison: Exploring Fraction Relationships
Comparing 3/4 and 2/3 helps illustrate the broader concept of fraction relationships. Understanding fraction comparisons extends to various applications, including:
- Problem Solving: Many real-world problems involve comparing parts of a whole, such as determining which portion of a pizza is larger or comparing progress on a project.
- Data Analysis: Fractions are frequently used in data representation and analysis, requiring the ability to compare fractional values to understand trends and patterns.
- Measurement: Fractions are integral to various measurement systems, including imperial units, requiring the ability to compare fractional measurements (e.g., comparing 3/4 inch to 2/3 inch).
Frequently Asked Questions (FAQ)
-
Q: Are there other ways to compare fractions? A: Yes, other methods include using number lines, converting to percentages, and using fraction calculators.
-
Q: What if the fractions have a common numerator instead of a common denominator? A: If the numerators are the same, the fraction with the smaller denominator is the larger fraction. For example, 2/3 > 2/5 because thirds are larger than fifths.
-
Q: How do I compare fractions with different signs (positive and negative)? A: A positive fraction is always greater than a negative fraction. When comparing two negative fractions, the fraction with the smaller absolute value (ignoring the negative sign) is the larger fraction. For example, -1/2 > -3/4.
-
Q: Can I use a calculator to compare fractions? A: Yes, most calculators have the functionality to perform fraction calculations and comparisons. Convert fractions to decimals or use the fraction comparison feature if available.
-
Q: Why is understanding fraction comparison important? A: Mastering fraction comparison builds a solid foundation for advanced mathematical concepts, including algebra, geometry, and calculus. It's a fundamental skill applicable to numerous real-world scenarios.
Conclusion: Mastering Fraction Comparison
The question "Is 3/4 bigger than 2/3?" serves as a springboard to understanding the various methods for comparing fractions. Through visual representation, finding common denominators, converting to decimals, and cross-multiplication, we've explored different approaches to determine that 3/4 is indeed larger than 2/3. Understanding these methods empowers you to confidently compare any two fractions, strengthening your mathematical foundation and preparing you for more advanced mathematical concepts and real-world applications. Remember to choose the method that best suits your understanding and the complexity of the fractions you're comparing. Practice regularly, and you'll quickly master this essential skill.
Latest Posts
Latest Posts
-
Saint Mary Margaret Catholic Church
Sep 16, 2025
-
1 Tablespoon Cinnamon In Grams
Sep 16, 2025
-
How Far Is Five Miles
Sep 16, 2025
-
Molecular Mass Of 1 Butanol
Sep 16, 2025
-
Nursing Care Plan For Psychosocial
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Is 3/4 Bigger Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.