What Is 15 Of 60
couponhaat
Sep 16, 2025 · 5 min read
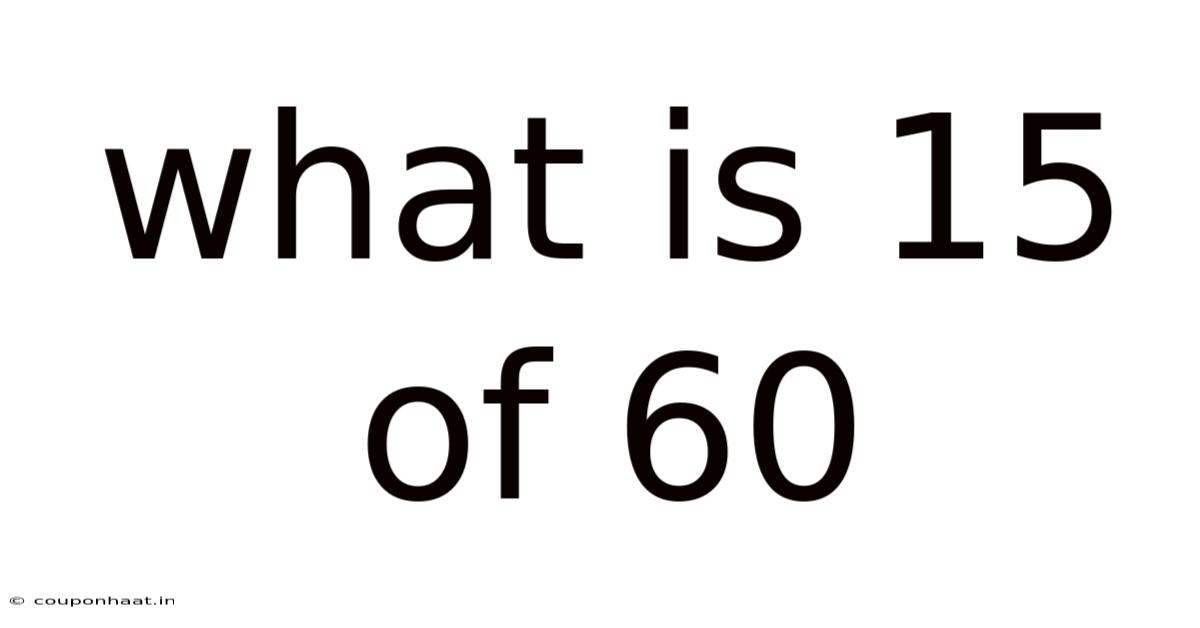
Table of Contents
What is 15 of 60? Unpacking Fractions, Percentages, and Ratios
What is 15 of 60? This seemingly simple question opens the door to a world of mathematical concepts, including fractions, percentages, and ratios. Understanding how to solve this, and similar problems, is crucial for everyday life, from calculating discounts to understanding financial reports. This article will not only answer the question directly but will delve into the underlying mathematical principles, providing a comprehensive understanding for learners of all levels.
Understanding the Fundamentals: Fractions, Percentages, and Ratios
Before we tackle "What is 15 of 60?", let's establish a firm foundation in the core mathematical concepts involved.
1. Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator represents the total number of parts in the whole. For example, 1/2 (one-half) means you have one part out of a total of two parts.
2. Percentages: A percentage is a way of expressing a fraction as a portion of 100. The symbol "%" represents "per cent" or "out of 100." To convert a fraction to a percentage, you divide the numerator by the denominator and multiply the result by 100. For example, 1/2 is equal to (1/2) * 100 = 50%.
3. Ratios: A ratio compares two or more quantities. It shows the relative size of one quantity to another. Ratios can be expressed in several ways: using a colon (e.g., 1:2), as a fraction (e.g., 1/2), or using the word "to" (e.g., 1 to 2). All these represent the same relationship.
Solving "What is 15 of 60?"
Now, let's address the central question: What is 15 of 60? This can be interpreted in several ways, each leading to a different representation of the relationship between 15 and 60.
1. As a Fraction: "15 of 60" can be interpreted as the fraction 15/60. This represents 15 parts out of a total of 60 parts. This fraction can be simplified by finding the greatest common divisor (GCD) of 15 and 60, which is 15. Dividing both the numerator and the denominator by 15 gives us the simplified fraction 1/4.
2. As a Percentage: To express 15/60 as a percentage, we divide the numerator (15) by the denominator (60): 15 ÷ 60 = 0.25. Then, we multiply the result by 100: 0.25 * 100 = 25%. Therefore, 15 is 25% of 60.
3. As a Ratio: The ratio of 15 to 60 can be written as 15:60 or 15/60. Simplifying this ratio, as we did with the fraction, gives us the simplified ratio 1:4. This means that for every one part, there are four parts in total.
Different Interpretations and Applications
The phrase "What is 15 of 60?" could also be interpreted in a slightly different context, depending on the situation. For instance:
-
Finding a Part of a Whole: If you have 60 apples and you take 15, you have taken 15/60 or 1/4 or 25% of the apples.
-
Proportions: The problem could represent a proportion. For example, if 15 out of 60 students passed an exam, what percentage passed? The answer remains 25%.
-
Scaling: Imagine a map with a scale of 1:4. If a distance on the map measures 15 cm, the actual distance would be 60 cm (15 x 4). Here, 15 represents a scaled-down version of 60.
Expanding the Understanding: Working with Fractions, Percentages, and Ratios
To further solidify your understanding, let's explore some related concepts and techniques:
1. Simplifying Fractions: Always simplify fractions to their lowest terms. This makes them easier to understand and compare. To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator and divide both by it.
2. Converting Between Fractions, Percentages, and Decimals: Being able to easily convert between these forms is essential.
* **Fraction to Percentage:** Divide the numerator by the denominator and multiply by 100.
* **Percentage to Fraction:** Divide the percentage by 100 and simplify the resulting fraction.
* **Decimal to Fraction:** Write the decimal as a fraction with a denominator of a power of 10 (e.g., 0.25 = 25/100). Then simplify the fraction.
* **Fraction to Decimal:** Divide the numerator by the denominator.
3. Solving Proportions: Proportions involve finding an unknown value in a relationship between two ratios. Cross-multiplication is a common method for solving proportions. For example, if 15/60 = x/100, then cross-multiplying gives 1500 = 60x, and solving for x gives x = 25.
4. Applying these Concepts to Real-World Problems: These mathematical concepts are ubiquitous in everyday life. Consider these examples:
* **Calculating Discounts:** A 25% discount on a $100 item means you save $25 (25% of $100).
* **Understanding Financial Statements:** Financial reports often use percentages and ratios to represent key performance indicators (KPIs).
* **Cooking and Baking:** Following recipes often involves working with fractions and ratios.
* **Map Reading:** Understanding map scales requires working with ratios.
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to calculate percentages?
A1: The easiest way is to use a calculator. However, for simple percentages, you can also use mental math techniques, such as finding 10% (divide by 10) and then scaling up or down from there.
Q2: How can I improve my skills in working with fractions?
A2: Practice is key. Start with simple fractions and gradually work your way up to more complex ones. Use visual aids, such as diagrams or pie charts, to help you visualize fractions.
Q3: Why are ratios important?
A3: Ratios are important because they allow us to compare different quantities and see their relative sizes. This is essential in many fields, including science, engineering, and finance.
Conclusion
The seemingly simple question, "What is 15 of 60?", provides a fertile ground for exploring fundamental mathematical concepts. By understanding fractions, percentages, and ratios, and mastering the techniques for converting between them, you equip yourself with essential tools for navigating everyday situations and tackling more complex mathematical problems. The answer, in its various forms – 1/4, 25%, or 1:4 – represents not just a numerical solution but a deeper understanding of proportional relationships. This knowledge empowers you to confidently tackle a wide range of mathematical and real-world challenges. Remember that consistent practice and applying these concepts to real-world scenarios are key to solidifying your understanding and building confidence in your mathematical abilities.
Latest Posts
Latest Posts
-
Lays Of Ancient Rome Book
Sep 16, 2025
-
Discharge Of A Capacitor Equation
Sep 16, 2025
-
Popular Rhythm And Blues Songs
Sep 16, 2025
-
Little Red Riding Hood Book
Sep 16, 2025
-
What Is A Textual Feature
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.