What Is 25 Of 50
couponhaat
Sep 17, 2025 · 6 min read
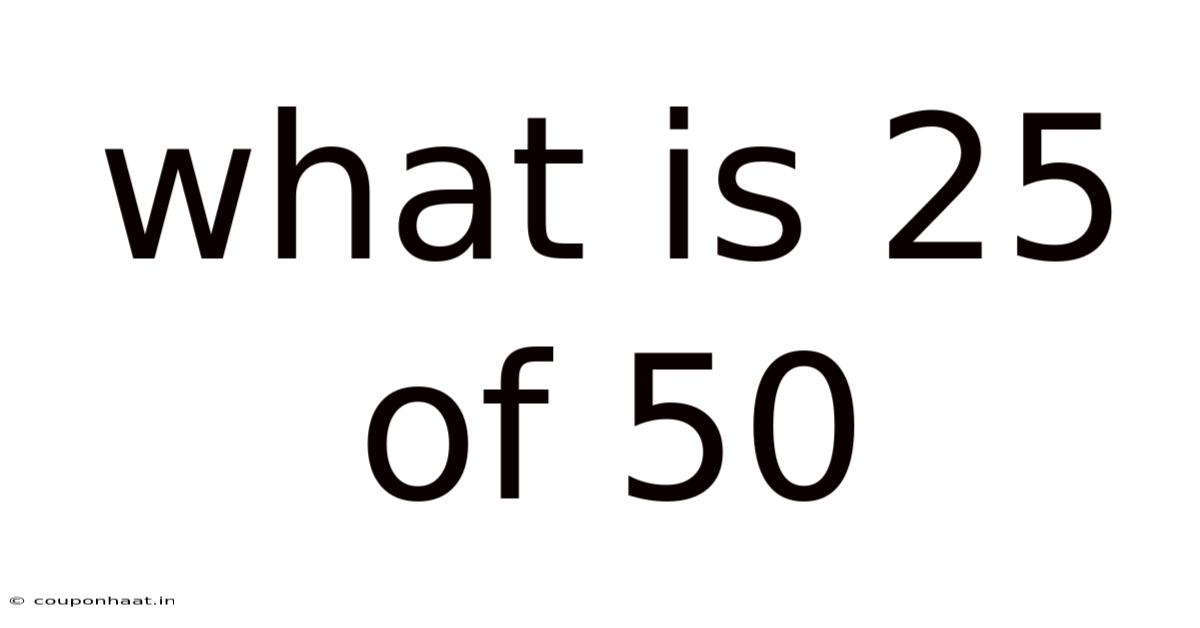
Table of Contents
What is 25 of 50? Understanding Fractions, Percentages, and Ratios
This seemingly simple question, "What is 25 of 50?", opens the door to a deeper understanding of fundamental mathematical concepts like fractions, percentages, and ratios. It's more than just a simple calculation; it's a gateway to understanding how these concepts relate to each other and how they are used in everyday life. This article will delve into the various ways to solve this problem, explain the underlying principles, and provide practical examples to solidify your understanding.
Understanding the Question: Different Interpretations
The phrasing "25 of 50" can be interpreted in several ways, all of which are mathematically valid but lead to different results depending on the context. Let's explore these interpretations:
-
25 as a part of 50: This is the most common interpretation. It asks what fraction or percentage 25 represents when compared to the whole, which is 50.
-
25 multiplied by 50: While less likely given the phrasing, this interpretation involves calculating 25 x 50. This is a straightforward multiplication problem.
-
25 divided by 50: This interpretation involves calculating 25/50. This will yield a decimal value representing the fraction.
We will focus primarily on the first interpretation, as it best reflects the typical understanding of the question.
Method 1: Finding the Fraction
The simplest way to understand "25 of 50" is to express it as a fraction. A fraction represents a part of a whole. In this case, 25 is the part, and 50 is the whole. Therefore, the fraction is written as:
25/50
This fraction can be simplified by finding the greatest common divisor (GCD) of 25 and 50, which is 25. Dividing both the numerator (top) and the denominator (bottom) by 25 gives us:
25/50 = 1/2
Therefore, 25 is one-half (1/2) of 50.
Method 2: Calculating the Percentage
To express "25 of 50" as a percentage, we first calculate the fraction as shown above (25/50 = 1/2). Then, we convert this fraction to a percentage by multiplying it by 100%:
(25/50) * 100% = 50%
Therefore, 25 represents 50% of 50. This means that 25 constitutes half of the total value of 50.
Method 3: Using Decimal Representation
We can also represent "25 of 50" as a decimal. This is done by dividing 25 by 50:
25 ÷ 50 = 0.5
The decimal value 0.5 is equivalent to the fraction 1/2 and the percentage 50%.
Understanding the Underlying Concepts
The problem of "25 of 50" illustrates several key mathematical concepts:
1. Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts, and the denominator indicates the total number of equal parts that make up the whole. Simplifying fractions involves reducing the numerator and denominator to their lowest common terms.
2. Percentages: Percentages are a way of expressing a fraction or decimal as a proportion of 100. The percentage symbol (%) means "per hundred." Converting a fraction to a percentage involves multiplying the fraction by 100%.
3. Ratios: Ratios compare two quantities. The ratio of 25 to 50 can be expressed as 25:50 or 25/50. Like fractions, ratios can be simplified by dividing both quantities by their greatest common divisor. In this case, the simplified ratio is 1:2.
4. Proportionality: The relationship between 25 and 50 is proportional. This means that they maintain a constant ratio. If you double 25 (to 50), you also double 50 (to 100), and the ratio remains the same (1:2).
Real-World Applications
Understanding fractions, percentages, and ratios is crucial in various real-world scenarios:
-
Shopping: Calculating discounts, sales tax, and comparing prices. For example, a 50% discount on a $50 item means a $25 saving.
-
Cooking: Following recipes that require specific proportions of ingredients. A recipe that calls for a 1:2 ratio of sugar to flour means that for every one unit of sugar, you use two units of flour.
-
Finance: Calculating interest rates, loan repayments, and investment returns. Understanding percentages is essential for managing personal finances.
-
Science: Expressing concentrations, measurements, and experimental results. Scientists often use ratios and percentages to report their findings.
Expanding the Understanding: Proportions and Solving for Unknowns
Let's extend the concept further by introducing problems where an unknown value needs to be found. For instance:
Problem: If 25 represents 50% of a certain number, what is that number?
This problem can be solved using proportions. We can set up the proportion:
25/x = 50/100
Where 'x' represents the unknown number. Cross-multiplying, we get:
25 * 100 = 50 * x
2500 = 50x
x = 2500 / 50
x = 50
Therefore, 25 is 50% of 50. This demonstrates the inverse relationship between fractions, percentages, and the underlying quantities.
Frequently Asked Questions (FAQ)
Q1: What if the numbers were larger or more complex? The same principles apply. You would still express the relationship as a fraction, simplify it if possible, and then convert it to a percentage or decimal as needed. For example, to find what 75 is of 150, you would calculate 75/150, simplify to 1/2, and then express it as 50%.
Q2: Can I use a calculator for these calculations? Absolutely! Calculators are useful for simplifying complex fractions and calculating percentages quickly. However, understanding the underlying concepts remains crucial.
Q3: What are some common mistakes to avoid? A common mistake is incorrectly setting up the fraction. Ensure the "part" is in the numerator and the "whole" is in the denominator. Another mistake is forgetting to multiply by 100% when converting a fraction to a percentage.
Q4: How can I improve my understanding of fractions, percentages, and ratios? Practice is key! Work through various problems, both simple and complex. Use online resources, textbooks, and practice worksheets to solidify your understanding.
Conclusion
The seemingly simple question, "What is 25 of 50?", provides a rich opportunity to explore the interconnectedness of fundamental mathematical concepts—fractions, percentages, and ratios. Mastering these concepts is crucial for success in various academic and professional fields. By understanding how these concepts relate to each other and by applying them to real-world scenarios, you can confidently tackle more complex mathematical problems and develop a stronger foundation in quantitative reasoning. Remember to always focus on understanding the underlying principles, rather than just memorizing formulas or procedures. The ability to solve such problems isn't just about getting the right answer; it's about understanding the why behind the calculation, which makes you more resourceful in various situations.
Latest Posts
Latest Posts
-
Red Riding Hood Super Why
Sep 17, 2025
-
How To Describe A Music
Sep 17, 2025
-
Carte De La Republique Dominicaine
Sep 17, 2025
-
Dollar Car Rental Yyz Airport
Sep 17, 2025
-
Where Are U In German
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.