What Is 60 Of 80
couponhaat
Sep 16, 2025 · 5 min read
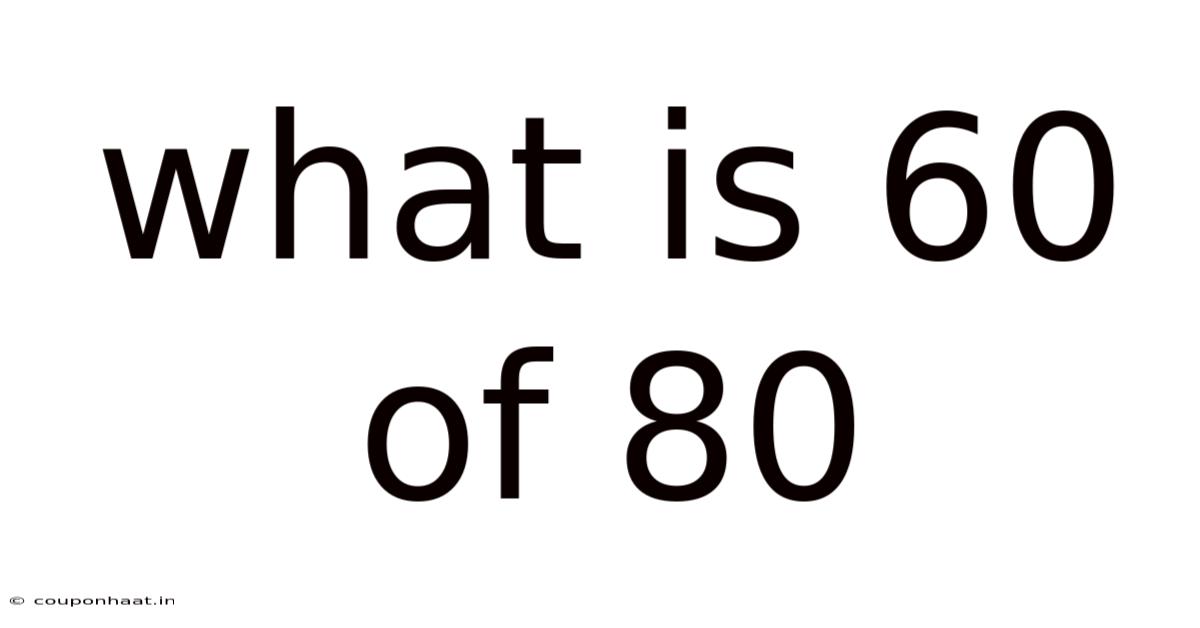
Table of Contents
What is 60% of 80? A Deep Dive into Percentages and Their Applications
Finding 60% of 80 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to calculate percentages, and more importantly, why we use them, opens doors to a vast world of applications across various fields, from finance and statistics to everyday decision-making. This article will not only answer the question "What is 60% of 80?" but also explore the underlying concepts, different calculation methods, and real-world examples demonstrating the significance of percentage calculations.
Understanding Percentages: The Foundation
A percentage is a fraction or a ratio expressed as a number out of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of a hundred." Therefore, 60% literally means 60 out of 100, or 60/100. This fraction can be simplified to 3/5. Understanding this fundamental concept is crucial for all percentage calculations.
Calculating 60% of 80: Three Methods
There are several ways to calculate 60% of 80. Let's explore three common methods:
Method 1: Using the Fraction Method
As we established, 60% is equivalent to the fraction 60/100 or 3/5. To find 60% of 80, we simply multiply 80 by the fraction 3/5:
80 x (3/5) = (80 x 3) / 5 = 240 / 5 = 48
Therefore, 60% of 80 is 48.
Method 2: Using Decimal Conversion
Percentages can also be easily converted to decimals. To convert a percentage to a decimal, simply divide the percentage by 100. In this case, 60% becomes 60/100 = 0.6. Now, multiply this decimal by 80:
80 x 0.6 = 48
Again, we arrive at the answer: 48.
Method 3: Using Proportions
This method utilizes the concept of proportions, setting up an equation to solve for the unknown value. We can set up a proportion as follows:
60/100 = x/80
To solve for x (which represents 60% of 80), we cross-multiply:
60 * 80 = 100 * x
4800 = 100x
x = 4800 / 100
x = 48
This method reinforces the underlying relationship between percentages and fractions, demonstrating the equivalence between the different approaches.
Beyond the Calculation: Real-World Applications
The ability to calculate percentages is not just an academic exercise; it's a fundamental skill with numerous practical applications. Let's look at some examples:
-
Finance: Calculating interest on loans or savings accounts, determining discounts on purchases, understanding tax rates, analyzing investment returns, and calculating profit margins all rely heavily on percentage calculations. For instance, if a store offers a 60% discount on an item originally priced at $80, the discount amount is $48, resulting in a final price of $32.
-
Statistics and Data Analysis: Percentages are ubiquitous in data representation and interpretation. Survey results, election polls, and economic indicators are frequently expressed as percentages to provide a clear and concise understanding of proportions and trends. For example, if a survey shows that 60% of 80 respondents prefer a particular product, it indicates that 48 respondents favor that product.
-
Science and Engineering: Percentage calculations are crucial in many scientific and engineering applications. For example, determining the efficiency of a machine, calculating the concentration of a solution, or analyzing experimental results often involves expressing values as percentages. Consider a chemical reaction where 60% of 80 grams of a reactant is converted into a product; this translates to 48 grams of product formation.
-
Everyday Life: We encounter percentages in numerous everyday scenarios. Calculating tips at restaurants, understanding sales tax, determining the percentage of completion of a project, or even simply comparing prices often requires percentage calculations.
Common Percentage Calculations and Formulas
Understanding the basic formula for calculating percentages is essential for tackling various percentage-related problems. The general formula is:
Percentage = (Part / Whole) x 100
Where:
- Part: Represents the specific portion of the whole you are interested in.
- Whole: Represents the total amount.
This formula can be rearranged to solve for other unknowns:
- To find the Part: Part = (Percentage/100) x Whole
- To find the Whole: Whole = (Part x 100) / Percentage
Troubleshooting Common Percentage Errors
Even experienced mathematicians can sometimes stumble on percentage calculations. Here are some common pitfalls to avoid:
-
Confusing Percentage and Decimal: Always ensure you correctly convert between percentages and decimals before performing calculations. A common mistake is using the percentage directly in calculations without converting it to a decimal or fraction.
-
Incorrect Order of Operations: Follow the order of operations (PEMDAS/BODMAS) carefully, especially when dealing with multiple operations within a calculation.
-
Rounding Errors: Be mindful of rounding errors, particularly when dealing with multiple steps in a calculation. Rounding at intermediate steps can lead to inaccuracies in the final result. It's often better to retain more decimal places during calculations and round only at the very end.
Frequently Asked Questions (FAQ)
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, subtract the original value from the new value, divide the result by the original value, and multiply by 100. For a percentage decrease, the process is the same, but the result will be negative.
Q: What if I need to calculate more complex percentage problems involving multiple percentages?
A: For multiple percentages, break down the calculation into smaller, manageable steps. Always address each percentage individually before combining the results.
Q: Are there any online tools or calculators that can help with percentage calculations?
A: Yes, many free online percentage calculators are available. These tools can be helpful for quick calculations and verification of manual calculations.
Conclusion: Mastering the Art of Percentages
Calculating 60% of 80, while seemingly straightforward, serves as a gateway to understanding the broader application of percentages. Mastering percentage calculations is not just about solving arithmetic problems; it's about developing a crucial skill applicable across numerous disciplines and everyday situations. By understanding the underlying principles and various calculation methods, you'll be equipped to confidently tackle percentage-related challenges, making informed decisions in various aspects of life. Remember to practice regularly and familiarize yourself with the different methods to build proficiency and avoid common errors. The ability to work comfortably with percentages will undoubtedly enhance your problem-solving skills and analytical capabilities.
Latest Posts
Latest Posts
-
Saint Mary Margaret Catholic Church
Sep 16, 2025
-
1 Tablespoon Cinnamon In Grams
Sep 16, 2025
-
How Far Is Five Miles
Sep 16, 2025
-
Molecular Mass Of 1 Butanol
Sep 16, 2025
-
Nursing Care Plan For Psychosocial
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.