X 2 Y 2 Z
couponhaat
Sep 15, 2025 · 6 min read
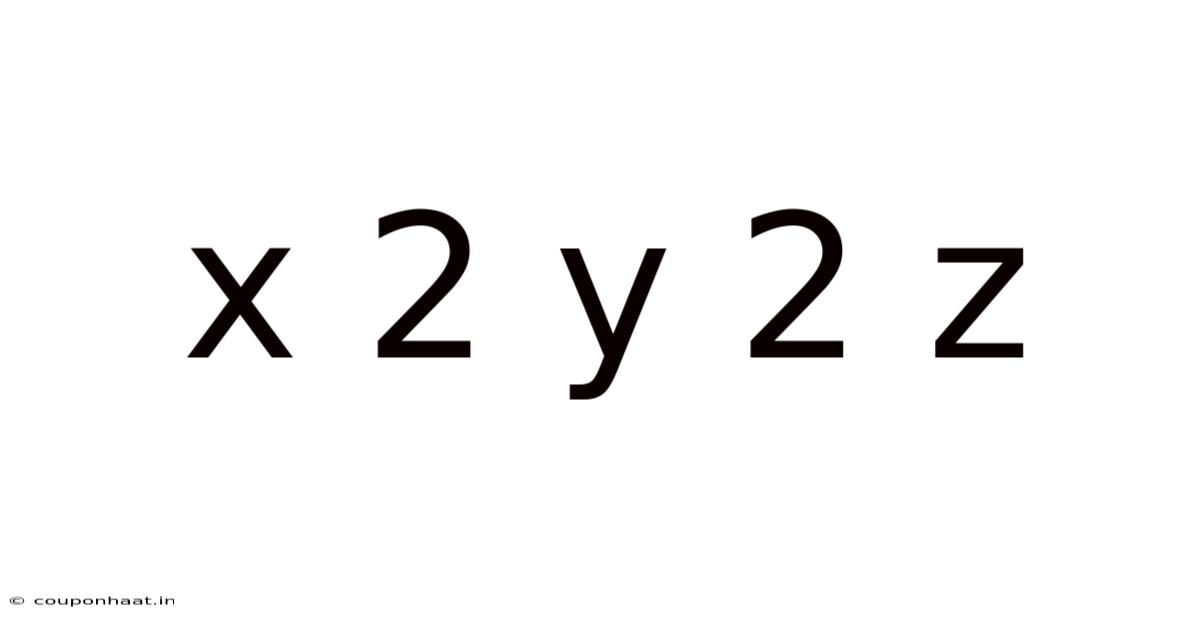
Table of Contents
Understanding x² + y² + z²: A Deep Dive into Sums of Squares
This article explores the mathematical expression x² + y² + z², focusing on its properties, applications, and significance in various fields. We'll delve into its geometric interpretations, its role in three-dimensional coordinate systems, and how it relates to other mathematical concepts. Understanding this seemingly simple equation opens doors to a richer comprehension of algebra, geometry, and even physics. We'll cover the basics for beginners and delve into more advanced concepts for those seeking a deeper understanding.
Introduction: What is x² + y² + z²?
At its core, x² + y² + z² represents the sum of the squares of three variables: x, y, and z. These variables can represent any real numbers, or in more advanced contexts, complex numbers or even vectors. While simple in appearance, this expression holds significant weight in various mathematical and scientific disciplines. It is fundamentally linked to concepts like distance, Pythagorean theorem extensions, and the representation of points in three-dimensional space. This seemingly simple equation provides the foundation for understanding many complex calculations in various mathematical and scientific fields.
Geometric Interpretation: The 3D Pythagorean Theorem
The true power of x² + y² + z² becomes clear when we visualize it geometrically. Imagine a three-dimensional coordinate system with the origin (0, 0, 0). Let's place a point P at coordinates (x, y, z). The expression x² + y² + z² then represents the square of the distance between the origin and point P.
This is a direct extension of the Pythagorean theorem, which deals with right-angled triangles in two dimensions. In 2D, the distance between the origin (0,0) and a point (x,y) is √(x² + y²). Adding the z-coordinate adds another dimension and extends this principle to three dimensions. Therefore, the distance from the origin to point P(x, y, z) is given by:
Distance = √(x² + y² + z²)
This formula is fundamental in numerous applications, from calculating distances between objects in 3D space to understanding the magnitude of vectors. The expression x² + y² + z² itself represents the square of this distance, a crucial element in many calculations.
Applications in Three-Dimensional Coordinate Systems
The expression x² + y² + z² is central to describing points and distances within a three-dimensional Cartesian coordinate system. Every point in 3D space can be uniquely identified using an ordered triple (x, y, z). The distance of this point from the origin, as we've seen, is determined using our expression. This is vital for:
-
3D Graphics and Computer-Aided Design (CAD): Calculating distances, rotations, and transformations of objects in 3D space relies heavily on the distance formula derived from x² + y² + z².
-
Physics and Engineering: Calculating forces, velocities, and accelerations of objects in three-dimensional space often involve determining distances and magnitudes, directly making use of this expression.
-
Mapping and Navigation: GPS systems and other navigational tools use three-dimensional coordinate systems and distance calculations based on the principle of this formula to pinpoint locations and determine distances between points.
Understanding the Equation in Different Contexts
The meaning and application of x² + y² + z² can vary slightly depending on the mathematical context.
-
Real Numbers: When x, y, and z are real numbers, the expression represents a scalar value, the square of the Euclidean distance in 3D space.
-
Vectors: If x, y, and z represent the components of a vector v = (x, y, z), then x² + y² + z² equals the squared magnitude (or squared norm) of the vector, often denoted as ||v||². The magnitude itself is √(x² + y² + z²).
-
Complex Numbers: If x, y, and z are complex numbers, the interpretation requires more nuanced consideration of the complex plane and potentially involves concepts of modulus and complex conjugate. The simple geometric interpretation of distance won't directly apply here.
Advanced Applications and Related Concepts
The seemingly simple equation x² + y² + z² underlies more complex mathematical concepts:
-
Spheres: The equation x² + y² + z² = r² represents a sphere of radius r centered at the origin in three-dimensional space. This is a direct consequence of the distance formula. Any point (x, y, z) satisfying this equation lies on the surface of the sphere.
-
Quadratic Forms: The expression x² + y² + z² is a special case of a quadratic form. Quadratic forms are homogeneous polynomial expressions of degree two in multiple variables, and their study is crucial in linear algebra and other advanced areas of mathematics.
-
Ellipsoids: By modifying the equation, we can represent ellipsoids which are three-dimensional counterparts of ellipses. For example, (x²/a²) + (y²/b²) + (z²/c²) = 1 represents an ellipsoid with semi-axes a, b, and c.
-
Multidimensional Spaces: The concept extends easily beyond three dimensions. In n-dimensional space, the analogous equation would be x₁² + x₂² + ... + xₙ², representing the squared Euclidean distance from the origin.
Solving Equations Involving x² + y² + z²
Solving equations involving x² + y² + z² often depends on the context. For instance:
-
Finding Points at a Specific Distance: If we are given an equation like x² + y² + z² = 25, we know that the solution set represents all points that are a distance of 5 units from the origin (a sphere with radius 5). Finding specific points on this sphere would require additional constraints or information.
-
Simultaneous Equations: If we have a system of equations involving x² + y² + z² along with other equations in x, y, and z, solving it may involve substitution, elimination, or other algebraic techniques. The complexity of the solution depends heavily on the form of the other equations.
Frequently Asked Questions (FAQ)
Q1: What is the difference between x² + y² + z² and √(x² + y² + z²)?
A1: x² + y² + z² represents the square of the distance from the origin to the point (x, y, z). √(x² + y² + z²) represents the actual distance itself.
Q2: Can x, y, and z be negative numbers?
A2: Yes, x, y, and z can be any real numbers, including negative numbers. The squaring operation eliminates the negative sign, contributing positively to the overall sum.
Q3: How is this equation used in physics?
A3: In physics, it is used extensively in calculating the magnitude of vectors (such as velocity, force, or displacement) in three-dimensional space, and in calculations involving distance and energy.
Q4: What happens if one or more of the variables are zero?
A4: If one or more variables are zero, the equation simplifies accordingly. For example, if z = 0, the equation becomes x² + y², which represents the square of the distance in a two-dimensional plane.
Conclusion: A Foundation for Higher Mathematics
The expression x² + y² + z² might seem simple at first glance, but its significance extends far beyond its initial appearance. Its geometric interpretation as the square of the distance in 3D space underpins a wealth of applications in various fields. Understanding this equation provides a solid foundation for grasping more complex concepts in algebra, geometry, and other branches of mathematics and science. From calculating distances in 3D graphics to understanding the magnitude of vectors in physics, its influence is pervasive and undeniable. Its study encourages a deeper appreciation for the interconnectedness of seemingly disparate mathematical concepts and the beauty of mathematical unity. Its significance lies not only in its immediate applications but also in its role as a cornerstone for advanced mathematical studies. The journey from a basic understanding to a deeper comprehension of this equation opens a window to the richness and elegance of mathematics.
Latest Posts
Latest Posts
-
80 000 Pounds To Tons
Sep 15, 2025
-
Helen Of Troys Mother Crossword
Sep 15, 2025
-
Life Cycle Of A Penguin
Sep 15, 2025
-
Defined Benefits Vs Defined Contribution
Sep 15, 2025
-
Past Tense Of To Pet
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 Z . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.